ลิเนียร์รีเกรสชั่น (Linear Regression)
เขียนโดย ดร.จักรกฤษณ์ แสงแก้ว วันที่ 21 กรกฎาคม 2562
บทนำ
- Linear Regession คือ การนำข้อมูลที่ได้มาคำนวณหาสมการเพื่อแทนลักษณะของข้อมูลนั้น ๆ - Simple Linear Regression คือ การนำข้อมูล 2 ชุด มาทำการหาสมการเพื่อแทนลักษณะข้อมูลของตัวแปรทั้ง 2 - Multiple Linear Regression คือ การนำข้อมูลมากกว่า 2 ชุด มาทำการหาสมการเพื่อแทนลักษณะข้อมูลของตัวแปรทั้งหมด ตัวแปรที่เกิดจากรีเกรสชั่น - R-Square หรือ Coefficient of determination มีค่าระหว่าง 0-1 ควรมีค่ามากกว่า 0.6 - Adjusted R-Square คือ การนำข้อมูลออก 1 ตัวแล้วคำนวณ R-Square ใหม่ ถ้าค่า R-Square และ Adjusted R-Square ต่างกันไม่มากถือว่าข้อมูลปกติดี แต่ถ้า Adjust R-Square มีค่าสูงคือข้อมูลที่นำมาวิเคราะห์มีจำนวนน้อยเกินไป - Coefficients คือ ค่าสัมประสิทธ์ที่มีผลต่อตัวแปรนั้น ๆ - P-value คือ ค่าความน่าจะเป็นมีค่าระหว่าง 0-1 ถ้ามีค่ามากกว่า 0.05 หมายถึงตัวแปรนั้นไม่มีความจำเป็นต้องนำมาใช้ในการสร้างสมการรีเกรสชั่น
1. Simple Linear Regression
- Simple Linear Regression เป็นการสร้างสมการเส้นตรงจากข้อมูลตัวเลข 2 ชุด คือ 1) ตัวแปรอิสระ \( x \) 2) ตัวแปรตาม \( \hat{Y} \)
- รูปแบบของสมการ Simple Linear Regression เขียนได้ดังนี้
$$ \hat{Y} = \alpha + \beta * x $$
$$\beta =\frac{ \sum{xy} - \frac{\sum{x}\sum{y}}{n}}{ \sum{x^2} - n (\bar{x})^2 }$$
$$\alpha = \bar{y} - \beta (\bar{x}) $$
%pylab inline
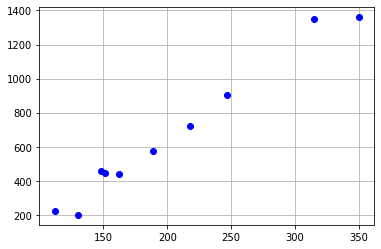
x = np.array([112,130,148,151,162,189,218,247,315,350])
y = np.array([225,200,459,445,439,577,722,903,1350,1360])
plt.plot(x,y,'bo')
plt.grid(True)
n = x.size
xy = x*y
x_square = x**2
sp = sum(xy) - ((sum(x)*sum(y))/n)
ss = sum(x_square) - n * x.mean() **2
beta = sp/ss
alpha = y.mean() - beta * (x.mean())
print('beta = ' ,beta)
print('alpha = ', alpha)
print('สมการเส้นตรงของข้อมูลชุดนี้คือ : y = alpha + beta * (x)')
print('สมการเส้นตรงของข้อมูลชุดนี้คือ : y = %f + %f * (x)'%(alpha,beta))
ผลลัพธ์ :
beta = 5.171599134963733 alpha = -377.69734508966667 สมการเส้นตรงของข้อมูลชุดนี้คือ : y = alpha + beta * (x) สมการเส้นตรงของข้อมูลชุดนี้คือ : y = -377.697345 + 5.171599 * (x)
การใช้งาน Simple Linear Regression ด้วย Scikit Learn
ในหัวข้อนี้จะใช้งานไลบรารี่ Scikit-Learn, Panda และ Seaborn ซึ่งเป็นไลบรารี่สำหรับภาษาไพธอน สำหรับงานวิเคราะห์ข้อมูลและการเรียนรู้ของเครื่องจักร โดยสามารถดาวน์โหลดใช้งานได้โดยไม่มีค่าใช้จ่าย - Scikit-Learn สำหรับงานด้านการเรียนรู้ของเครื่องจักร (Machine Learning) เว็บไซต์ตั้งอยู่ที่ https://scikit-learn.org - Panda สำหรับการเตรียมและจัดการข้อมูลเพื่อการประมวลผล เว็บไซต์ตั้งอยู่ที่ https://pandas.pydata.org - Seaborn สำหรับการแสดงผลข้อมูลในรูปวิชวลทำงานบน matplotlib สามารถแสดงผลข้อมูลเกี่ยวกับสถิติต่าง ๆ ของข้อมูลได้ เว็บไซต์ตั้งอยู่ที่ https://seaborn.pydata.org/
import pandas as pd
import seaborn as sns
%pylab inline
x = np.array([112,130,148,151,162,189,218,247,315,350])
y = np.array([225,200,459,445,439,577,722,903,1350,1360])
data = {'x':x, 'y':y}
df = pd.DataFrame(data)
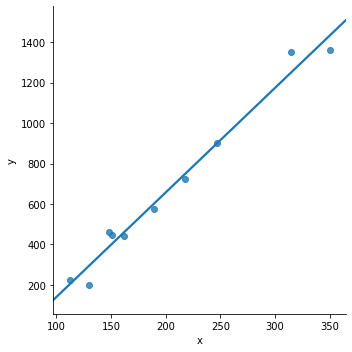
sns.lmplot(x='x',y='y',data=df,ci=None)
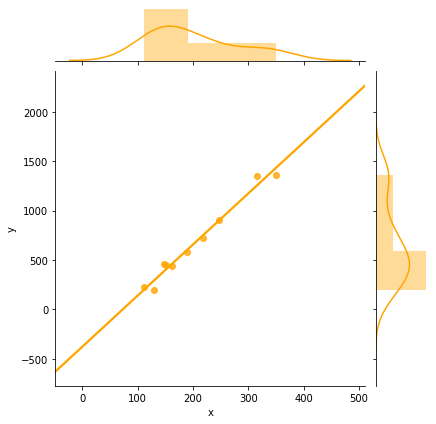
sns.jointplot(x='x',y='y',data=df, kind='reg', ci=None,color='orange')
from sklearn.linear_model import LinearRegression
model = LinearRegression()
print(model)
df.info()
x = df[['x']] # เขียนโดยระบุชื่อคอลัมน์ได้อีกรูปแบบ คือ y = df.x
y = df[['y']] # เขียนโดยระบุชื่อคอลัมน์ได้อีกรูปแบบ คือ y = df.y
model.fit(x,y)
model.score(x,y) # R-squared ของโมเดล
model.intercept_
model.coef_
อธิบาย : บรรทัดที่ 1-2 : ขอใช้ไลบรารี่ pandas และ seaborn สำหรับจัดการดาต้าเซ็ตและการแสดงกราฟิกวิชวลไลซ์ บรรทัดที่ 3 : %pylab inline เป็นการขอใช้ matplotlib และ numpy ฯลฯ เมื่อใช้คำสั่งนี้แล้วไม่ต้อง import numpy และ matplotlib บรรทัดที่ 4-5 : ประกาศตัวแปร 2 ชุด คือ x และ y บรรทัดที่ 6 : สร้างตัวแปรดิกชันนารี เพื่อนำไปใช้เป็นอินพุตให้กับดาต้าเฟรมต่อไป บรรทัดที่ 7 : สร้างตัวแปร df เป็นชนิดดาต้าเฟรมโดยนำข้อมูลมาจากบรรทัดที่ 6 ดังนั้นจะมี 2 คอลัมน์คือ x และ y บรรทัดที่ 8 : การพล็อตกราฟด้วยฟังก์ชั่น lmplot() ซึ่งเป็นลีเนียร์โมเดล ผลลัพธ์จะได้เป็นเส้นตรงแทนข้อมูล x และ y โดยกำหนด ci=None (confidence interval) คือ ไม่ต้องแสดง บรรทัดที่ 9 : การพล็อตกราฟด้วยฟังก์ชั่น jointplot() โดยแสดงค่าความถี่ออกมาด้วย ในตัวอย่างนี้คือ ความถี่ของของตัวแปร x และ y
บรรทัดที่ 11 : ประกาศขอใช้งาน LinearRegression ภายในไลบรารี่ Scikit-Learn บรรทัดที่ 12 : สร้างอ็อบเจ็คของคลาส LinearRegression เพื่อใช้สำหรับสร้างสมการเส้นตรงต่อไป บรรทัดที่ 13 : พิมพ์การตั้งค่าพารามิเตอร์ของโมเดล ผลลัพธ์จะแสดงคำว่า LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False) หมายถึง ทำการคัดลอกค่า X และกำหนดให้ใช้จุดตัดแกน Y และไม่ต้องนอมัลไลซ์ข้อมูล บรรทัดที่ 14 : แสดงข้อมูลเกี่ยวกับดาต้าเฟรมที่ใช้งาน ในตัวอย่างนี้แสดงผลลัพธ์ เช่น ตัวแปรที่อยู่ภายใน x และ y และจำนวนข้อมูล 10 ตัว มีชนิดข้อมูลเป็นเลขจำนวนเต็ม 32 บิต เป็นต้น แสดงผลลัพธ์ได้ดังนี้RangeIndex: 10 entries, 0 to 9 Data columns (total 2 columns): x 10 non-null int32 y 10 non-null int32 dtypes: int32(2) memory usage: 160.0 bytes บรรทัดที่ 16-17 : กำหนดตัวแปร x และ y โดยจะทับข้อมูลเดิมที่ประกาศในบรรทัดที่ 4-5 เพื่อจะนำไปใช้ในการสร้างลิเนียร์รีเกรสชั่นโมเดลต่อไป บรรทัดนี้ผู้อ่านสามารถกำหนดเป็นตัวแปรอื่นได้เพื่อป้องกันการสับสน บรรทัดที่ 19 : สร้างโมเดลลิเนียร์รีเกรสชั่นด้วยฟังก์ชั่น fit() โดยป้อนข้อมูลตัวแปรอิสระและตัวแปรตาม ตามลำดับ บรรทัดที่ 21 : เป็นการพิมพ์ค่า R-square ของโมเดล ซึ่งในตัวอย่างนี้มีค่า 0.98 บรรทัดที่ 22 : แสดงค่าจุดตัดแกน y หรือค่า \(\alpha\) ของสมการลิเนียร์รีเกรสชั่น ซึ่งมีค่า -377.69 บรรทัดที่ 23 : แสดงค่าสัมประสิทธิ์ Coefficient หรือค่า \(\beta\) ของสมการลิเนียร์รีเกรสชั่น มีค่า 5.17
2. Multiple Linear Regression
- Multiple Linear Regressoin คือ การสร้างสมการเส้นตรงเพื่อแทนลักษณะข้อมูลของกลุ่มตัวแปร มากกว่า 2 ตัวขึ้นไป
- สมการของ Multiple Linear Regression คือ \(Y = \beta_{0} + \beta_{1}x_{1} + \beta_{2}x_{2} + \epsilon\)
- สำหรับการคำนวณหาค่า \(\beta_{1}, \beta_{2} .. \beta_{n}\) ดำเนินการในลักษณะเดียวกับ Simple Linear Regression
การใช้งาน Multiple Linear Regression ด้วย Python และ Scikit Learn
ในหัวข้อนี้เป็นการใช้งานลีเนียร์รีเกรสชั่นหลายตัวแปร (Multiple Linear Regression) โดยใช้ดาต้าเซ็ตการโฆษณาและยอดขาย ประกอบด้วยการโฆษณา จาก 3 แหล่ง ได้แก่ โทรทัศน์ วิทยุ หนังสือพิมพ์ 1. ตัวแปรตาม (dependent variable) คือ ยอดขาย 2. ตัวแปรอิสระหรือตัวแปรต้น (independent variable) คือ ก) โฆษณากับโทรทัศน์ ข) โฆษณากับวิทยุ ค) โฆษณากับหนังสือพิมพ์ วัตถุประสงค์ของการทำ Multiple Linear Regression คือ การสร้างสมการเส้นตรงจากข้อมูลที่เก็บรวบรวมมา โดยมีตัวแปรอิสระมากกว่า 1 ตัวขึ้นไป เขียนโปรแกรมด้วยภาษาไพธอนและ Scikit-Learn ได้ดังนี้
import pandas as pd
import seaborn as sns
%pylab inline
df = pd.read_csv("https://raw.githubusercontent.com/dsdi/dataset/master/th-advertising.csv", usecols=[1,2,3,4])
sns.set(font="Kanit-Light",font_scale=2)
sns.set_context("paper", font_scale=1.5)
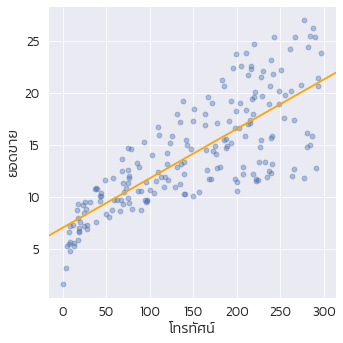
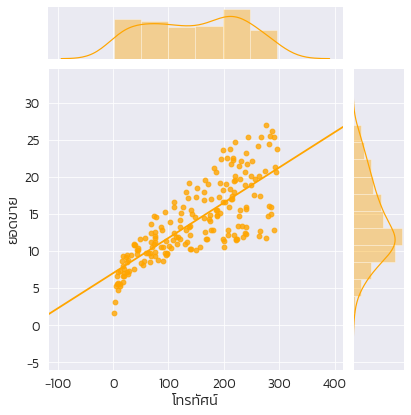
sns.lmplot(x='โทรทัศน์',y='ยอดขาย', data=df, ci=None, scatter_kws={'alpha':0.4}, line_kws={'color':'orange'})
sns.jointplot(x='โทรทัศน์',y='ยอดขาย', data=df, kind='reg', ci=None,color='orange')
from sklearn.linear_model import LinearRegression
x = df.drop(columns=['ยอดขาย'])[:160]
y = df['ยอดขาย'][:160]
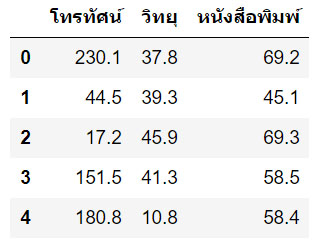
x.head()
model = LinearRegression()
model.fit(x,y)
model.score(x,y) #R-Squared
model.intercept_
model.coef_ # สัมประสิทธิ์ ของ ทีวี วิทยุ หนังสือพิมพ์
model.predict([[250,40,70]]) # โฆษณาด้วย ทีวี 250, วิทยุ 40 และหนังสือพิมพ์ 70 จะมียอดขาย 22
model.predict([[250,40,70],
[50,40,45],
[20,50,70]])
x_test = df.drop(columns=['ยอดขาย'])[160:]
x_test.head()
y_predict = model.predict(x_test)
print(y_predict)
dc = pd.concat([df[160:].reset_index(), pd.Series(y_predict,name='พยากรณ์')],axis='columns')
dc
คำอธิบาย : บรรทัดที่ 1-2 : ขอใช้ไลบรารี่ pandas และ seaborn บรรทัดที่ 3 : ขอใช้งาน matplotlib และ numpy ผ่านคำสั่ง %pylab inline บรรทัดที่ 5 : อ่านดาต้าเซ็ตเข้ามาซึ่งเก็บไว้ใน github ในขั้นตอนนี้ต้องเชื่อมต่ออินเตอร์เน็ตเพื่อโหลดข้อมูล บรรทัดที่ 6 : กำหนดฟอนต์ kanit-light เพื่อแสดงผลภาษาไทยบนกราฟซึ่งต้องติดตั้งลงในคอมพิวเตอร์ก่อนการใช้งาน หากสามารถใช้ฟอนต์ Tahoma แทนได้ บรรทัดที่ 7 : กำหนดขนาดฟอนต์ใหญ่ขึ้น 1.5 เท่า บรรทัดที่ 8 : พล็อตเส้นตรงด้วยฟังก์ชั่น lmplot() ซึ่งเป็น linear model โดยกำหนดค่า "โทรทัศน์" เป็นตัวแปรต้น และ "ยอดขาย" เป็นตัวแปรตาม ใช้ข้อมูลจากตัวแปร df และไม่ต้องแสดง ci (confidence interval) กำหนดให้พล็อตแบบ scatter มีค่าโปร่งแสง 40 เปอร์เซ็นต์ และระบายสีเส้นด้วยสีส้ม บรรทัดที่ 9 : พล็อตข้อมูลโดยแสดงความถี่ของข้อมูลด้านบนและด้านข้างของกราฟเพื่อแสดงความหนาแน่นของข้อมูล โดยใช้ฟังก์ชั่น jointplot() และใช้ตัวแปรต้น คือ โทรทัศน์ ส่วนตัวแปรตาม คือ ยอดขาย กำหนดพารามิเตอร์ kind เป็นชนิด "reg" (regression) ไม่ต้องแสดง confidence interval และระบายสีส้มลงบนเส้นลีเนียร์รีเกรสชั่น
บรรทัดที่ 11 : ขอใช้งานคลาส LinearRegression จากไลบรารี่ Scikit-Learn บรรทัดที่ 12 : สร้างตัวแปรต้นเก็บไว้ใน x ให้มีข้อมูลเพียง 3 คอลัมน์ โดยลบคอลัมน์ "ยอดขาย" ออกไป และดึงข้อมูลมาเพียง 160 เรคคอร์ด บรรทัดที่ 13 : สร้างตัวแปรตามเก็บไว้ใน y ให้มีข้อมูลเพียง 1 คอลัมน์ คือ "ยอดขาย" และดึงข้อมูลมาก 160 เรคคอร์ด บรรทัดที่ 14 : แสดงข้อมูล header ของตัวแปรต้น ออกมา ซึ่งจะประกอบด้วย โทรทัศน์ วิทยุ หนังสือพิมพ์ ดังนี้
บรรทัดที่ 15 : สร้างอินสแตนท์ของคลาส LinearRegression() ชื่อ model เพื่อใช้สำหรับการสร้างโมเดลโดยสามารถตั้งชื่ออื่นตามที่ต้องการ ได้ เช่น my_linear_regression_model เป็นต้น
บรรทัดที่ 16 : คำสั่ง fit() เป็นการสร้างรีเกรสชั่นโมเดลโดยระบุตัวแปรต้นและตัวแปรอิสระลงไป ในตัวอย่างนี้ x เป็นตัวแปรต้น ส่วน y เป็นตัวแปรอิสระ
บรรทัดที่ 17-19 : แสดงค่า R-Square ด้วยคำสั่ง score(x,y) ตามด้วยแสดงค่า \(\beta_{0}\) หรือค่าจุดตัดแกน y (intercept_) และสุดท้ายแสดงค่าสัมประสิทธิ์ของตัวแปรซึ่งเก็บไว้ใน model.coef_ มีจำนวนเท่ากับตัวแปรอิสระ ได้แก่ สัมประสิทธิ์การโฆษณาด้วยโทรทัศน์ วิทยุ และหนังสือพิมพ์ตามลำดับ
บรรทัดที่ 20 : คำนวณค่า ยอดขาย จากโมเดลที่สร้างขึ้นด้วยการป้อนข้อมูลใหม่เข้าไปเพื่อพยากรณ์ว่ายอดขายจะเท่ากับเท่าไร โดยระบุโทรทัศน์ (250), วิทยุ (40) และหนังสือพิมพ์ (70) พบว่าโมเดลที่ได้ทำนายผลลัพธ์ยอดขายมีค่า 21.89
บรรทัดที่ 21-23 : เป็นการคำนวณ ยอดขาย เหมือนบรรทัด 20 แต่ส่งข้อมูลไปพร้อมกัน 3 แถว ผลลัพธ์ แสดงดังนี้ array([21.89282947, 12.46601233, 12.82406754])
บรรทัดที่ 24 : สร้างตัวแปร x_test สำหรับนำส่วนที่เหลือจากแถวที่ 161 - 200 มาคำนวณ ยอดขาย โดยส่งเข้าไปให้ฟังก์ชั่น predict()
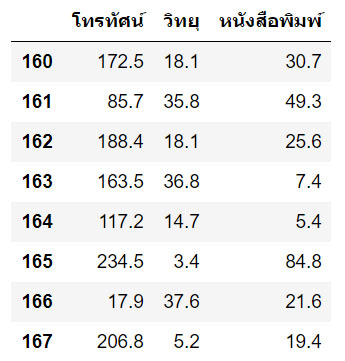
บรรทัดที่ 25 : แสดงข้อมูลของตัวแปร x_test ออกมาด้วยคำสั่ง x_test.head(8) เมื่อเลข 8 คือจำนวนเรคคอร์ดที่ต้องการแสดงผลลลัพธ์ออกมาเพียงบางส่วน ดังนี้
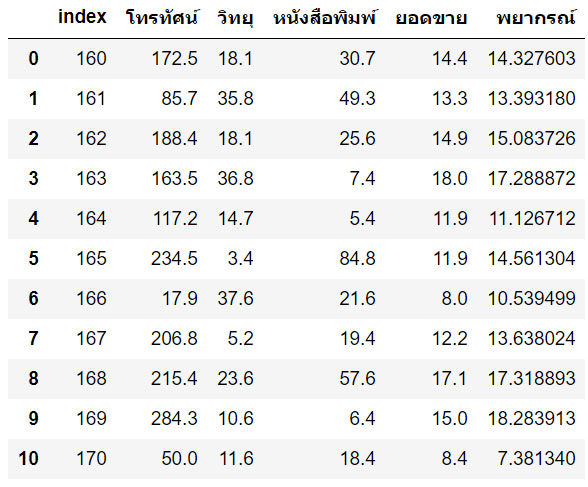
บรรทัดที่ 27 : แสดงผลลัพธ์การคำนวณ ยอดขาย จากแถวที่ 161 ถึง 200 ออกมา บรรทัดที่ 29 : สร้างตัวแปรใหม่ ชื่อ dc โดยเพิ่มผลลัพธ์ที่คำนวณได้ในบรรทัดที่ 27 ขึ้นมาเป็นอีก 1 คอมลัมน์ ชื่อ "พยากรณ์" บรรทัดที่ 30 : แสดงผลตัวแปร dc หลังจากเพิ่มคอลัมน์ "พยากรณ์" เข้าไป แสดงผลลัพธ์ได้ ดังนี้
การใช้งาน Multiple Linear Regression ด้วย Python และ Statsmodels
ในหัวข้อนี้เป็นการใช้งาน Multi Linear Regression ด้วยภาษาไพธอนและใช้ไลบรารี่อีกตัวหนึ่งที่ชื่อว่า statsmodel ให้ผลการวิเคราะห์ข้อมูลทางสถิติละเอียดกว่า scikit-learn พิจารณาตัวอย่างต่อไปนี้
import statsmodels.api as sm
import statsmodels.formula.api as smf
df = pd.read_csv("https://raw.githubusercontent.com/dsdi/dataset/master/en-advertising.csv", usecols=[1,2,3,4])
model = smf.ols(formula="Sales ~ TV + Radio + Newspaper", data=df[:160]).fit()
print(model.summary())
ผลลัพธ์ :
OLS Regression Results
==============================================================================
Dep. Variable: Sales R-squared: 0.896
Model: OLS Adj. R-squared: 0.894
Method: Least Squares F-statistic: 448.7
Date: Mon, 22 Jul 2019 Prob (F-statistic): 1.80e-76
Time: 12:47:30 Log-Likelihood: -310.02
No. Observations: 160 AIC: 628.0
Df Residuals: 156 BIC: 640.3
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 2.9490 0.358 8.236 0.000 2.242 3.656
TV 0.0473 0.002 29.965 0.000 0.044 0.050
Radio 0.1799 0.010 18.149 0.000 0.160 0.200
Newspaper -0.0009 0.007 -0.143 0.886 -0.014 0.012
==============================================================================
Omnibus: 52.610 Durbin-Watson: 2.120
Prob(Omnibus): 0.000 Jarque-Bera (JB): 128.997
Skew: -1.388 Prob(JB): 9.74e-29
Kurtosis: 6.412 Cond. No. 453.
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
อธิบาย : บรรทัดที่ 1-2 : ขอใช้ไลบรารี่ statsmodels บรรทัดที่ 3 : สร้างตัวแปรดาต้าเฟรมตั้งชื่อ df โดยโหลดข้อมูลดาต้าเซ็ตจากไฟล์ en-advertising.csv ใช้คอลัมน์ 1,2,3 และ 4 ตามลำดับ บรรทัดที่ 4 : สร้างโมเดลจากสูตร "Sales ~ TV + Radio + Newspaper" โดยใช้ข้อมูล 160 เรคอร์ดด้านบนจากทั้งหมด 200 เรคคอร์ด บรรทัดที่ 5 : แสดงรายละเอียดข้อมูลชุดนี้ ประกอบด้วยค่าสถิติหลายตัว ได้แก่ R-Squared และ Adjusted R-Squared ฯลฯ - ค่า p-value ช่วยให้มองเห็นว่า ตัวแปร newspaper มีค่า 0.886 ซึ่งไม่มีนัยสำคัญทางสถิติ หมายถึงตัวแปรดังกล่าวไม่จำเป็นต้องนำมาใช้ในการสร้างสมการจะยังคงให้ความถูกต้องไม่แตกต่างกัน
ศึกษาเพิ่มเติม
- https://sites.google.com/site/mystatistics01/home - https://www.youtube.com/user/RStatsInstitute/videos