การคำนวณทางคณิตศาสตร์

» การคำนวณเบื้องต้น บวก ลบ คูณ หาร
» ดาวน์โหลด MathCAD5
» หนังสือ Mathcad และ SPSS
» หนังสือ Mathcad
» ฟังก์ชั่นและการพล็อตกราฟ
» การโปรแกรมมิ่งสำหรับสถิติเบื้องต้น (Statistic)
» สัญลักษณ์ทางสถิติ
» ตัวแปรต้นและตัวแปรตาม
» ค่าแนวโน้มสู่ศูนย์กลาง
» รูปทรงของข้อมูล
» ความน่าจะเป็น (Probability)
» การเขียนโปรแกรมคำนวณค่าเฉลี่ย (Mean)
» การเขียนโปรแกรมคำนวณค่ามัธยฐาน (Median)
» การเขียนโปรแกรมคำนวณค่าฐานนิยม (Mode)
» การเขียนโปรแกรมคำนวณค่าเบี่ยงเบนมาตรฐาน (standard deviation)
» การเขียนโปรแกรมคำนวณค่าความแปรปรวน (Variance)
» การเขียนโปรแกรมคำนวณความเบ้ (Skewness)
» การเขียนโปรแกรมคำนวณค่าความโด่งของข้อมูล (kurtosis)
» การเขียนโปรแกรมอธิบายร้อยละ
» เส้นโค้งปกติ
» การคำนวณค่าเปอร์เซ็นต์ที่มากกว่าค่าที่กำหนด
» การคำนวณค่าเปอร์เซ็นต์ที่น้อยกว่าค่าที่กำหนด
» การเขียนโปรแกรมเพื่อคำนวณเปอร์เซ็นต์ของคะแนนที่อยู่ในช่วงที่กำหนด
» การคำนวณเปอร์เซ็นต์ของคะแนน
» การเขียนโปรแกรมพยากรณ์และจัดหมวดหมู่ข้อมูล
» การเขียนโปรแกรมคำนวณลีเนียร์รีเกรสชั่น (Linear Regression Equation) 
» อัลกอริทึมในการพยากรณ์ (Prediction Algorithms)
» การเขียนโปรแกรมจัดหมวดหมู่ประเภทผลไม้ด้วย Decision Tree
» การเขียนโปรแกรมจัดหมวดหมู่ภาพทะเลหรือภาพภูเขา

กิจกรรมที่ 1: การคำนวณคณิตศาสตร์

» ให้นิสิตคำนวณคณิตศาสตร์ บวก ลบ คูณ หาร ด้วย MathCAD5
» ดาวน์โหลด ดาวน์โหลด MathCAD5

คำนวณ	พิมพ์
\( 15 \times 3 = 45 \)	15*3=a
\( \frac{49}{7}=7 \)	49/7=a
\( 58+12=70 \)	58+12=a
\( 3.25-16.5=-13.25 \)	3.25-16.5=a
\( \frac{(42+13)\times 12}{100} = 6.6\)	(42+13)*12w/100=a
\( 2^2=4 \)	2^2=a
\( \sqrt{ 450+2}=21.26 \)	450+2w\=a
\( sin(\frac{\pi}{2}) =1 \)	SIN(cP/2):a
\( cos(\frac{\pi}{3}) =0.5 \)	COS(cP/3):a
\( tan(\frac{\pi}{4}) =1 \)	TAN(cP/4):a
\( adder(x,y):x+y \) \(adder(3,2)=5\)	ADDER(X,Y):X+Ya ADDER(3,2)=a

F(X)=a

กิจกรรมที่ 2: ฟังก์ชั่นและกราฟ

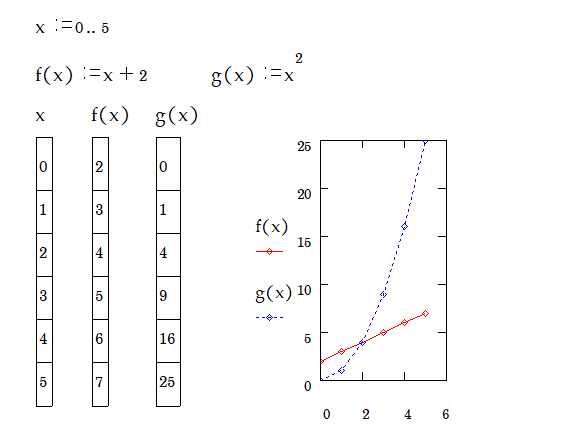
กิจกรรม: 2.1 ฟังก์ชั่น \( f(x) = x+2 \) และ \( g(x) = x^2 \)

» ฟังก์ชั่น เป็นการกำหนดกฎของผลลัพธ์ โดยที่ "กฎ" ที่นิยามฟังก์ชั่นอาจเป็น สูตร , ความสัมพันธ์ 
» แนวคิดของฟังก์ชั่นเป็นพื้นฐานของทุกสาขาที่เกี่ยวกับคณิตศาสตร์

คำสั่ง
» ให้นิสิตสร้างฟังก์ชั่น  \( f(x) = x+2 \) และ \( g(x) = x^2 \) 
» กำหนดค่าตัวแปร x ให้มีค่า 1 ถึง 5 โดยเพิ่มค่าทีละ 0.5
» แสดงค่าตัวแปร x และ f(x) และพล็อตกราฟ

คำนวณ	พิมพ์
\( f(x)=x+2 \)	F(X):X+2a
\( x:1;5 \)	X:1;5a
\( x= \)	X=a
\( f(x)= \)	F(X)=a

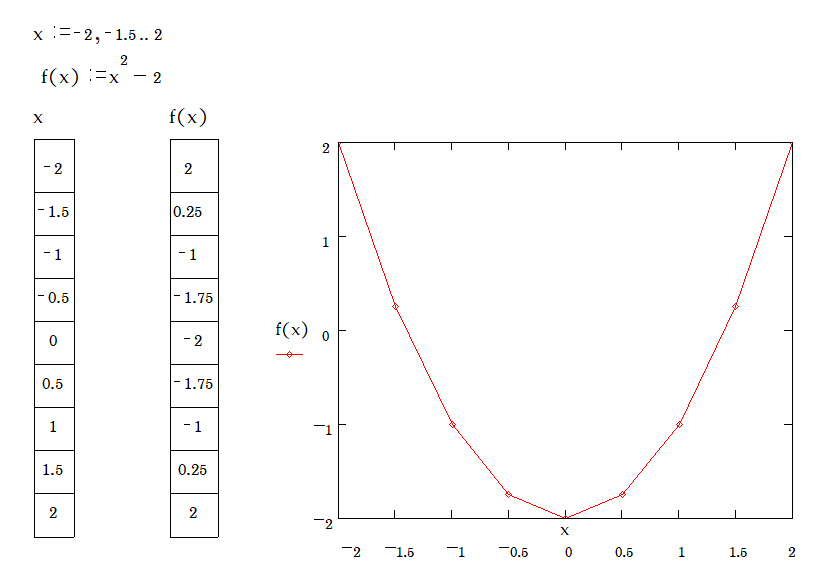
2.2 ฟังก์ชั่นและการพล็อตกราฟของฟังก์ชั่น \( f(x) = x^2 - 2 \)

คำสั่ง
» กำหนดค่าตัวแปร x มีค่า -2 ถึง 2 ลดลงทีละ 0.5
» สร้างฟังก์ชั่น \( f(x) = x^2 - 2 \)
» ให้แสดงค่าผลลัพธ์ของตัวแปร x และ f(x)
» พล็อตกราฟแสดงความสัมพันธ์ระหว่างตัวแปร x และ f(x) 

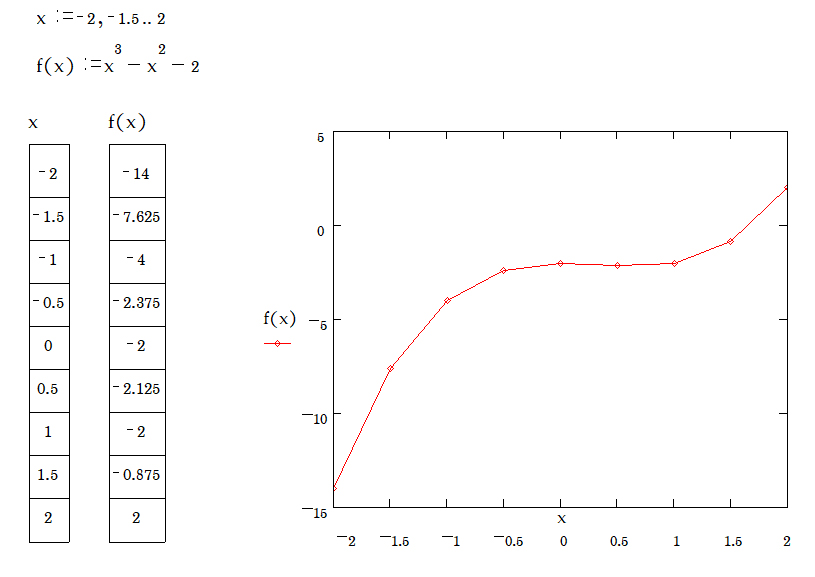
2.3 ฟังก์ชั่นและการพล็อตกราฟของฟังก์ชั่น \( f(x) = x^3 - x^2 - 2 \)

คำสั่ง
» กำหนดค่าตัวแปร x มีค่า -2 ถึง 2 ลดลงทีละ 0.5
» สร้างฟังก์ชั่น \( f(x) = x^3 - x^2 - 2 \)
» ให้แสดงค่าผลลัพธ์ของตัวแปร x และ f(x)
» พล็อตกราฟแสดงความสัมพันธ์ระหว่างตัวแปร x และ f(x) 

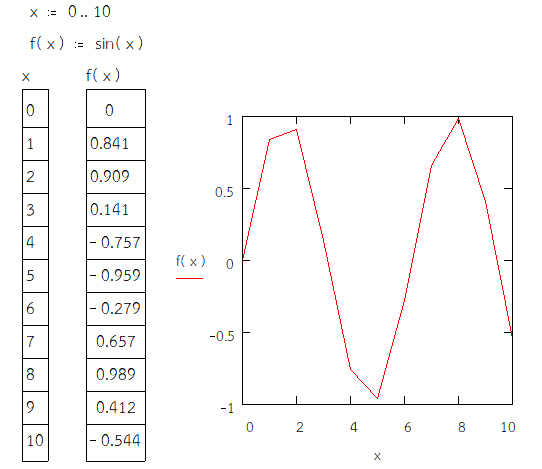
กิจกรรม: 2.4 ฟังก์ชั่นตรีโกณมิติ (Trigonon)

» ตรีโกณมิติ คือ คณิตศาสตร์ที่ศึกษาความสัมพันธ์ระหว่างความยาวและมุมของรูปสามเหลี่ยม

คำสั่ง
» กำหนดค่าตัวแปร x มีค่า 0 ถึง 10
» สร้างฟังก์ชั่น \( f(x) = sin(x) \)
» ให้แสดงค่าผลลัพธ์ของตัวแปร x และ f(x)
» พล็อตกราฟแสดงความสัมพันธ์ระหว่างตัวแปร x และ f(x) 

2.5 ฟังก์ชั่นและการพล็อตกราฟตรีโกณมิติ

คำสั่ง
» กำหนดค่าตัวแปร x มีค่า 0 ถึง \( 2 \times \pi \)
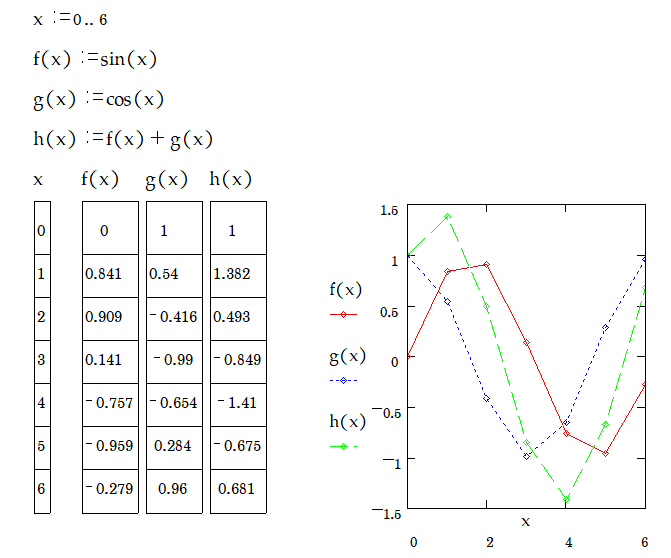
» สร้างฟังก์ชั่น f(x) = sin(x), g(x) = cos(x) และ h(x) = f(x) + g(x)
» ให้แสดงค่าผลลัพธ์ของตัวแปร x , f(x), g(x) และ h(x) ตามลำดับ
» พล็อตกราฟแสดงความสัมพันธ์ระหว่างตัวแปร x, f(x), g(x) และ h(x)

การโปรแกรมมิ่งสำหรับสถิติเบื้องต้น (Statistic)

» สถิติ (Statistic) คือ 1) การรวบรวมข้อมูล 2) การวิเคราะห์ข้อมูล 3) การตีความข้อมูล

» ประชากรและกลุ่มตัวอย่าง 1) ประชากร คือกลุ่มข้อมูลทั้งหมดที่เราสนใจ 2) กลุ่มตัวอย่าง คือ ข้อมูลกลุ่มย่อยที่เลือกออกมาศึกษา

» ข้อมูลแบ่งออกเป็น 2 ประเภท 
   1) ข้อมูลเชิงปริมาณ (Quantitative data) คือ ข้อมูลที่อยู่ในรูปตัวเลข (numerical data) ที่แสดงถึงปริมาณที่เป็นจำนวนเต็มหรือจำนวนนับ เช่น จำนวน รถยนต์ในกรุงเทพมหานคร จำนวนบุตรในครอบครัว เป็นต้น
   2) ข้อมูลเชิงคุณภาพ (Qualitative data) คือ ข้อมูลที่แสดงถึงสถานภาพ คุณลักษณะ หรือคุณสมบัติ เช่น เพศ เชื้อชาติ สถานภาพสมรส ศาสนา กลุ่มเลือด เป็นต้น

» ระดับการวัด 4 ระดับ 
   1) ระดับนามบัญญัติ (Nominal) เช่น เพศ ในห้องนี้มีชายกี่คน หญิงกี่คน ระดับนี้เป็นการวัดที่ต่ำที่สุด ทำได้เพียงบอกร้อยละ
   2) ระดับเรียงลำดับ (Ordinal)  เช่น  ชอบนายกเท่าไร  ชอบมากที่สุด (5) ชอบมาก (4) ปานกลาง (3) น้อย (2) ไม่ชอบเลย (1) เป็นต้น ตัวเลขพวกนี้เป็นระดับเรียงลำดับ
   3) ระดับช่วง (Interval) เช่น วัดค่าออกมาเป็นตัวเลขแต่ไม่มีศูนย์แท้ เช่น วัดค่าอุณหภูมิได้ 0 องศา ไม่ได้หมายความว่าไม่มีอุณหภูมิ
   4) ระดับอัตราส่วน (Ratio)  วัดค่าออกมาเป็นตัวเลขที่มีศูนย์แท้ เช่น เงินในกระเป๋า 0 บาท คือไม่มีเงินแม้แต่บาทเดียว เป็นต้น

» ประชากร (Population) คือ การเก็บรวบรวมข้อมูลจากข้อมูลทั้งหมด
» กลุ่มตัวอย่าง (Sample) คือ การเก็บรวบรวมข้อมูลบางส่วนที่เลือกออกมาจากประชากร
» ค่าพารามิเตอร์ (Parameter) คือ ค่าที่คำนวณมาจากข้อมูลประชากรทั้งหมด
» ค่าสถิติ (Statistics) คือ ค่าที่คำนวณมาจากกลุ่มตัวอย่าง โดยใช้ประมาณค่าพารามิเตอร์

สัญลักษณ์

» ค่าเฉลี่ย (Mean) ก) ค่าเฉลี่ยของประชากร เขียนแทนด้วย \( \mu \) ข) ค่าเฉลี่ยของกลุ่มตัวอย่าง เขียนแทนด้วย \( \bar{x} \)
» ค่าเบี่ยงเบนมาตรฐาน ก) ค่าเบี่ยงเบนมาตรฐานของประชากร เขียนแทนด้วย \( \sigma \) ข) ค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่าง เขียนแทนด้วย \( S \)
» ค่าความแปรปรวน ก) ค่าความแปรปรวนของประชากร เขียนแทนด้วย \( \sigma^2 \) ข) ค่าความแปรปรวนของกลุ่มตัวอย่าง เขียนแทนด้วย \( S^2 \)
» ค่าสัดส่วน ก) ค่าสัดส่วนของประชากร เขียนแทนด้วย \( p \) ข) ค่าสัดส่วนของกลุ่มตัวอย่าง เขียนแทนด้วย \( \hat{p} \)
» ค่าสหสัมพันธ์ (Correlation) ก) ค่าสหสัมพันธ์ของประชากร เขียนแทนด้วย \( \rho \) อ่านว่า rho ข) ค่าสหสัมพันธ์ของกลุ่มตัวอย่าง เขียนแทนด้วย \( r \)

ตัวแปรต้นและตัวแปรตาม

» ตัวแปรต้น มีชื่อเรียกที่แตกต่างกันไปตามตำราแต่ละเล่ม เช่น ตัวแปรอิสระ, ตัวแปรสาเหตุ 
» ตัวแปรตาม คือ ค่าผลลัพธ์
» จากตัวอย่างต่อไปนี้ \( f(x) = x^2 \) 
   คำถาม 1) ตัวแปร \( x \) คือ ตัวแปรอะไร ? ........................ (ตัวแปรต้น / ตัวแปรตาม)
   คำถาม 2) ตัวแปร \( f(x) \) คือ ตัวแปรอะไร ? ........................ (ตัวแปรต้น / ตัวแปรตาม)

ค่าแนวโน้มสู่ศูนย์กลาง

» ค่าแนวโน้มสู่ส่วนกลาง คือ การบอกค่ากลาง ๆ ของกลุ่มข้อมูลที่เก็บรวบรวมมา ได้แก่ 
1) ค่าเฉลี่ย (Mean) 
2) ค่าตำแหน่งข้อมูล ได้แก่ ก) ค่าฐานนิยม (Mode) ข) ค่ามัธยฐาน (Median) ค) เปอร์เซ็นต์ไทล์ คือ แบ่งข้อมูลเป็น 100 ส่วน (Percentiles) ง) ควอไทล์ คือแบ่งข้อมูลเป็น 4 ส่วน (Quartiles) จ) ค่าเดไซล์ คือ แบ่งข้อมูลเป็น 10 ส่วน (Deciles) 
3) การวัดการกระจาย ได้แก่ ก) ค่าพิสัย (Range) ข) ส่วนเบี่ยงเบนควอไทล์ (Quartile Deviation: Q.D.) ค) ส่วนเบี่ยงเบนเฉลี่ย (Average Deviation หรือ Mean Deviation: M.D.) ง) ส่วนเบี่ยงเบนมาตรฐาน (Standard Deviation: \( \sigma \) จ) ค่าความแปรปรวน 

รูปทรงของข้อมูล

» รูปทรงของข้อมูล บอกการกระจายตัวของข้อมูล
1) ความเบ้ (Skewness)
2) ความโด่ง (Kurtosis) ก) ถ้าค่าความโด่งน้อยกว่า 0.263 แสดงว่ารูปทรงเป็นแบบแบนราบ ข) ถ้าความโด่งมีค่ามากกว่า 0.263 แสดงว่ารูปทรงโด่งมาก ค) ถ้าความโด่งเท่ากับ 0.263 แสดงว่ารูปทรงมีความโด่งปกติ

ความน่าจะเป็น (Probability)

» การกระจายความน่าจะเป็นของประชากร คือ การกระจายค่าที่มีโอกาสเกิดเหตุการณ์ที่จะเกิดขึ้นได้
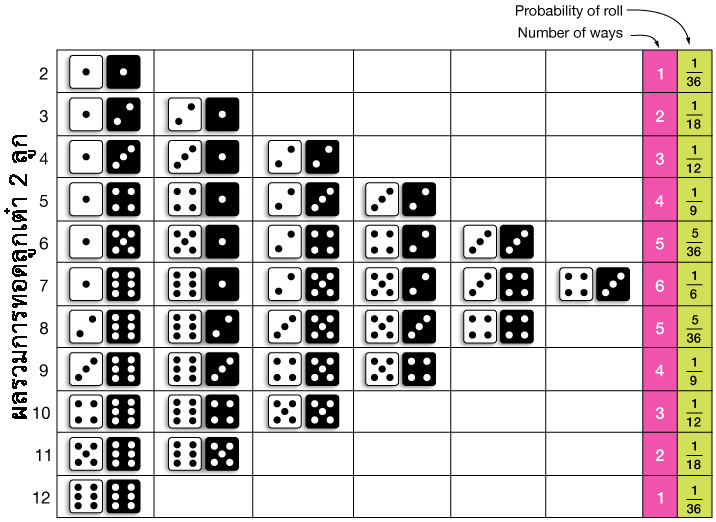
» พิจารณาความน่าจะเป็นของการทอดลูกเต๋า 2 ลูก

ความน่าจะเป็นของการทอดลูกเต๋า 2 ลูก

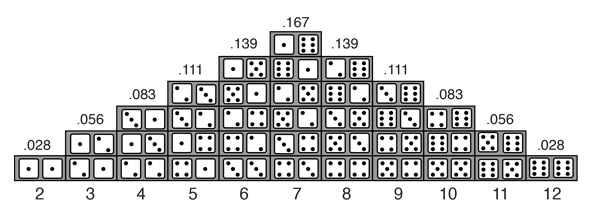
การกระจายตัวของโอกาสความน่าจะเป็นในการทอดลูกเต๋า 2 ลูก

x	2	3	4	5	6	7	8	9	10	11	12
P(x)	1/36	2/36	3/36	4/36	5/36	6/36	5/36	4/36	3/36	2/36	1/36

» ในการโยนลูกเต๋า 1 ลูก ผลลัพธ์มีโอกาสเกิดเท่าเทียมกัน แต่ในการโยนลูกเต๋าสองลูกความเป็นไปได้ของผลรวจะไม่เท่ากัน
» การที่จะทอดลูกเต๋า 2 ลูกแล้วได้ผลรวมเท่ากับ 7 มีได้มากถึง 6 วิธี 
» โอกาสที่ทอดลูกเต๋า 2 ลูก ได้ผลรวมเท่ากับ 2 มีความน่าจะเป็นเท่ากับ 0.028 (1/36)
» โอกาสที่ทอดลูกเต๋า 2 ลูก ได้ผลรวมเท่ากับ 3 มีความน่าจะเป็นเท่ากับ 0.056 (2/36)
» โอกาสที่ทอดลูกเต๋า 2 ลูก ได้ผลรวมเท่ากับ 4 มีความน่าจะเป็นเท่ากับ 0.083 (3/36)
» โอกาสที่ทอดลูกเต๋า 2 ลูก ได้ผลรวมเท่ากับ 5 มีความน่าจะเป็นเท่ากับ 0.111 (4/36)
» โอกาสที่ทอดลูกเต๋า 2 ลูก ได้ผลรวมเท่ากับ 6 มีความน่าจะเป็นเท่ากับ 0.139 (5/36)
» โอกาสที่ทอดลูกเต๋า 2 ลูก ได้ผลรวมเท่ากับ 7 มีความน่าจะเป็นเท่ากับ 0.167 (6/36)
» โอกาสที่ทอดลูกเต๋า 2 ลูก ได้ผลรวมเท่ากับ 8 มีความน่าจะเป็นเท่ากับ 0.139 (5/36)
» โอกาสที่ทอดลูกเต๋า 2 ลูก ได้ผลรวมเท่ากับ 9 มีความน่าจะเป็นเท่ากับ 0.111 (4/36)
» โอกาสที่ทอดลูกเต๋า 2 ลูก ได้ผลรวมเท่ากับ 10 มีความน่าจะเป็นเท่ากับ 0.083 (3/36)
» โอกาสที่ทอดลูกเต๋า 2 ลูก ได้ผลรวมเท่ากับ 11 มีความน่าจะเป็นเท่ากับ 0.056 (2/36)
» โอกาสที่ทอดลูกเต๋า 2 ลูก ได้ผลรวมเท่ากับ 12 มีความน่าจะเป็นเท่ากับ 0.028 (1/36)
» ผลรวมของความน่าจะเป็นรวมเท่ากับ 0.028 + 0.056 + 0.083 + 0.111 + 0.139 + 0.167 + 0.139 + 0.111 + 0.083 + 0.056 + 0.028 = 1.00

กิจกรรมที่ 3: การเขียนโปรแกรมคำนวณค่าเฉลี่ย \( \bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_{i} \)

» ค่าเฉลี่ย คือ ผลรวมของข้อมูลทั้งหมด / จำนวนข้อมูล

3.1 การเขียนโปรแกรมคำนวณค่าเฉลี่ย

x = [1,3,2]
n = len(x)
mean = sum(x)/n
print("ค่าเฉลี่ยของ %s เท่ากับ %.2f"%(str(x), mean))

ผลลัพธ์
ค่าเฉลี่ยของ [1, 3, 2] เท่ากับ 2.00

3.2 การเขียนฟังก์ชั่นคำนวณค่าเฉลี่ย

def ค่าเฉลี่ย(data):
   n = len(data)
   mean = sum(data)/n
   return mean

x = [1,3,2]
print("ค่าเฉลี่ย %s เท่ากับ %.2f"%(str(x), ค่าเฉลี่ย(x)))

ผลลัพธ์
ค่าเฉลี่ย [1, 3, 2] เท่ากับ 2.00

กิจกรรมที่ 4: การเขียนโปรแกรมคำนวณค่ามัธยฐาน (Median)

» ค่ามัธยฐาน หาได้จากนำข้อมูลมาเรียงลำดับจากน้อยไปมากหรือมากไปน้อย โดยมัธยฐานคือข้อมูลที่อยู่ตรงกลางพอดี
» ตัวอย่างข้อมูลดังนี้ [4.3, 2.9, 2.7, 4.1,  40.8, 3.4, 4.7, 3.7, 3.1, 4.7]

1) เรียงลำดับข้อมูลจากน้อยไปมากหรือมากไปน้อย  [2.7,   2.9,   3.1,   3.4,   3.7,  4.1,   4.3,   4.7,  4.7,  40.8] 
2) มัธยฐานข้อมูลที่อยู่ตำแหน่งกึ่งกลางข้อมูลที่เรียงลำดับแล้ว

มัฐยฐานมีค่า \( \frac{3.7 + 4.1}{2} = 3.9 \)

4.1 เขียนโปรแกรมคำนวณมัฐยฐาน (Median)

from math import ceil, floor

x = [4.3, 2.9, 2.7, 4.1,  40.8, 3.4, 4.7, 3.7, 3.1, 4.7]
x.sort()

p = floor(len(x)/2)
if len(x)/2 > p:
  print(x[ceil(len(x)/2)-1])
else:
  a = x[ceil(len(x)/2)-1]
  b = x[ceil(len(x)/2)]
  c = (a+b)/2
  print(c)

กิจกรรมที่ 5: การเขียนโปรแกรมคำนวณค่าฐานนิยม (Mode)

» ค่าฐานนิยม (Mode) คือค่าที่พบมากที่สุดในข้อมูล
» ตัวอย่างข้อมูล [4,2,1,3,1,2,1,5,1] 
- เลข 4 พบ 1 ครั้ง
- เลข 2 พบ 2 ครั้ง
- เลข 3 พบ 1 ครั้ง
- เลข 1 พบ 4 ครั้ง
ดังนั้น ค่า ฐานนิยม คือเลข 1 เพราะมีความถี่สูงสุดภายในตัวแปร x

5.1 เขียนโปรแกรมคำนวณฐานนิยม (Mode)

x = [4,2,1,3,1,2,1,5,1]

u = list(set(x))
max_found = max(list(map(lambda i: x.count(i), u)))

for i in u:
  if x.count(i) == max_found:
    print("ค่าฐานนิยม (mode) ที่พบมากที่สุดคือ %.2f พบ %d ครั้ง "%(i,max_found))

5.2 เขียนฟังก์ชั่นเพื่อคำนวณฐานนิยม (Mode)

def ฐานนิยม(data):
  u = list(set(x))
  max_found = max(list(map(lambda i: x.count(i), u)))

  for i in u:
    if x.count(i) == max_found:
      return i
      break

x = [4,2,1,3,1,2,1,5,1]
ฐานนิยม(x)

ผลลัพธ์
1

กิจกรรมที่ 6: การเขียนโปรแกรมคำนวณค่าเบี่ยงเบนมาตรฐาน \( sd = \sqrt{ \frac{ \sum |xi - \bar{x} |^2} {n} } \)

» \(s\) หรือ \( sd \) คือ ค่าเบี่ยงเบนมาตรฐาน
» \( \bar{x} \) คือ ค่าเฉลี่ย
» \( x_{i} \) คือ ข้อมูลลำดับที่ \( i \)
» \( n \) คือ จำนวนข้อมูล

6.1 เขียนโปรแกรมคำนวณค่าเบี่ยงเบนมาตรฐาน

x = [8, 5, 2, 4, 10, 1, 7, 3, 6, 9]
n = len(x)
mean = sum(x)/n
sd = sqrt(sum(list(map(lambda i: ((i-mean)**2)/(n), x))))
print("ค่าเบี่ยงเบนมาตรฐานของข้อมูล %s มีค่า %.2f"%(str(x), sd))

ผลลัพธ์
ค่าเบี่ยงเบนมาตรฐานของข้อมูล [8, 5, 2, 4, 10, 1, 7, 3, 6, 9] มีค่า 2.87

6.2 การเขียนฟังก์ชั่นคำนวณค่าเบี่ยงเบนมาตรฐาน

def ส่วนเบี่ยงเบนมาตรฐาน(data):
   n = len(data)
   mean = sum(data)/n
   sd = sqrt(sum(list(map(lambda i: ((i-mean)**2)/(n), data))))
   return sd

x = [8, 5, 2, 4, 10, 1, 7, 3, 6, 9]
ส่วนเบี่ยงเบนมาตรฐาน(x)

ผลลัพธ์
2.8722813232690143

กิจกรรมที่ 7: การเขียนโปรแกรมคำนวณค่าความแปรปรวน \( var = \frac{ \sum |xi - \bar{x} |^2} {n} \)

» ค่าความแปรปรวน (Variance) เป็นค่าที่ใช้วัดการกระจายข้อมูล

» \( var \) หรือ \( s^2 \) หรือ \(sd^2\) หรือ \( S^2 \) คือ ค่าความแปรปรวน (Variance)  
» \( \bar{x} \) คือ ค่าเฉลี่ย
» \( x_{i} \) คือ ข้อมูลลำดับที่ \( i \)
» \( n \) คือ จำนวนข้อมูล

7.1 เขียนโปรแกรมคำนวณค่าความแปรปรวน

x = [8, 5, 2, 4, 10, 1, 7, 3, 6, 9]
n = len(x)
mean = sum(x)/n
var = sum(list(map(lambda i: ((i-mean)**2)/(n), x)))
print("ค่าความแปรปรวนของข้อมูล %s มีค่า %.2f"%(str(x), var))

ผลลัพธ์
ค่าความแปรปรวนของข้อมูล [8, 5, 2, 4, 10, 1, 7, 3, 6, 9] มีค่า 8.25

7.2 การเขียนฟังก์ชั่นคำนวณค่าความแปรปรวน

def ความแปรปรวน(data):
   n = len(data)
   mean = sum(data)/n
   var = sum(list(map(lambda i: ((i-mean)**2)/(n), data)))
   return var

x = [8, 5, 2, 4, 10, 1, 7, 3, 6, 9]
ความแปรปรวน(x)

ผลลัพธ์
8.25

กิจกรรมที่ 8: การเขียนโปรแกรมบอกระดับความเบ้ของข้อมูล \( skewness = \frac{n}{(n-1)(n-2)} \sum(\frac{x_{i} - \bar{x}}{sd})^3 \)

» ถ้าในชั้นเรียนมีนิสิต 30 คน และได้เกรด A จำนวน 20 คน , เกรด B จำนวน 6 คน และเกรด C จำนวน 4 คน ลักษณะแบบนี้คือเกรดเฟ้อ ถ้านำมาพล็อตจะเห็นว่าข้อมูลมีการเบ้ (skewness)

การวิเคราะห์ค่าความเบ้
» ค่าความเบ้มีค่าเป็นลบ แสดงว่ารูปทรงเป็นแบบเบ้ซ้าย
» ค่าความเบ้มีค่าเป็นบวก แสดงว่ารูปทรงเป็นแบบเบ้ขวา
» ค่าความเบ้มีค่าเป็น 0 แสดงว่ารูปทรงเป็นแบบสมมาตร

8.1 การเขียนโปรแกรมคำนวณความเบ้

def ส่วนเบี่ยงเบนมาตรฐาน(data):
   n = len(data)
   mean = sum(data)/n
   sd = sqrt(sum(list(map(lambda i: ((i-mean)**2)/(n), data))))
   return sd


data = [10, 9, 10, 11, 12, 9, 11, 11, 8, 10]
n = len(data)
mean = sum(data)/n
sd = ส่วนเบี่ยงเบนมาตรฐาน(data)
skew = (n/((n-1)*(n-2))) * (sum(list(map(lambda i: ((i-mean)/sd)**3, data))))


skewness = ความเบ้(x)
print("ความเบ้ของ %s มีค่า %.2f"% (str(x), skewness))

ผลลัพธ์
ความเบ้ของ [10, 9, 10, 11, 12, 9, 11, 11, 8, 10] มีค่า -0.27

8.2 การสร้างฟังก์ชั่นเพื่อคำนวณความเบ้

def ความเบ้(data):
  n = len(data)
  mean = sum(data)/n
  sd = ส่วนเบี่ยงเบนมาตรฐาน(data)
  skew = (n/((n-1)*(n-2))) * (sum(list(map(lambda i: ((i-mean)/sd)**3, data))))
  return skew


x = [10, 9, 10, 11, 12, 9, 11, 11, 8, 10]
skewness = ความเบ้(x)
print("ความเบ้ของ %s มีค่า %.2f"% (str(x), skewness))

ผลลัพธ์
ความเบ้ของ [10, 9, 10, 11, 12, 9, 11, 11, 8, 10] มีค่า -0.27

กิจกรรมที่ 9: การเขียนโปรแกรมคำนวณค่าความโด่งของข้อมูล \( kurtosis = (\frac{n(n+1)}{(n-1)(n-2)(n-3)} \times \sum( \frac{x_{i} - \bar{x}}{sd} )^4) - ( \frac{3(n-1)^2} {(n-2)(n-3)}) \)

» ความโด่งของข้อมูล คือ ข้อมูลมีลักษณะเกาะกลุ่มกันหรือกระจายตัวของข้อมูล หากมีการเกาะกลุ่มกันมาก ๆ จะมีลักษณะโด่ง เช่น นักเรียน 30 คนได้เกรด C จำนวน 27 คน หมายความว่ามีลักษณะโด่งมากเพราะเกาะกลุ่มที่เกรด C เป็นต้น

เมื่อ \( \bar{x} \) คือ ค่าเฉลี่ยของข้อมูล
     \( x_{i} \) คือ ข้อมูลลำดับที่ \( i \)
     \( sd \) คือ ส่วนเบี่ยงเบนมาตรฐาน
     \( n \) คือ จำนวนข้อมูล

» ค่าความโด่งมีค่าน้อยกว่า 0.263 แสดงว่ารูปทรงเป็นแบบแบนราบ
» ค่าความโด่งมีค่ามากกว่า 0.263 แสดงว่ารูปทรงเป็นแบบโด่งมาก
» ค่าความโด่งมีค่าเท่ากับ 0.263 แสดงว่ารูปทรงเป็นแบบโด่งปกติ

9.1 การเขียนโปรแกรมคำนวณความโด่ง

data = [10, 9, 10, 11, 12, 9, 11, 11, 8, 10]
n = len(data)
s = ส่วนเบี่ยงเบนมาตรฐาน(data)
mean = ค่าเฉลี่ย(data)
k1 = (n*(n-1))/((n-1)*(n-2)*(n-3))
k2 = sum(list(map(lambda i: ((i-mean)/s)**4, data)))
k3 =  ((3*(n-1)**2)/((n-2)*(n-3)))
print("ความโด่งของ %s มีค่าเท่ากับ %.2f"%(str(data), kurtosis(data)))  

ผลลัพธ์
ความโด่งของ [10, 9, 10, 11, 12, 9, 11, 11, 8, 10] มีค่าเท่ากับ -0.33

9.2 การสร้างฟังก์ชั่นเพื่อคำนวณความโด่ง

def kurtosis(data):
  n = len(data)
  s = ส่วนเบี่ยงเบนมาตรฐาน(data)
  mean = ค่าเฉลี่ย(data)
  k1 = (n*(n-1))/((n-1)*(n-2)*(n-3))
  k2 = sum(list(map(lambda i: ((i-mean)/s)**4, data)))
  k3 =  ((3*(n-1)**2)/((n-2)*(n-3)))
  return (k1*k2)-k3

data = [10, 9, 10, 11, 12, 9, 11, 11, 8, 10]
k = kurtosis(data)
print("ความโด่งของ %s มีค่าเท่ากับ %.2f"%(str(data), kurtosis(data)))

ผลลัพธ์
ความโด่งของ [10, 9, 10, 11, 12, 9, 11, 11, 8, 10] มีค่าเท่ากับ -0.33

กิจกรรมที่ 10: การเขียนโปรแกรมอธิบายร้อยละ

»  ตัวแปร นามบัญญัติ (Nominal) และ ตัวแปรอันดับ (Order) จะใช้ค่าสถิติร้อยละในการบรรยาย เช่น ตัวแปรเพศ

def กิจกรรม_10():
  x = [30, 25, 30, 29, 32, 27, 28, 30, 32, 35, 27, 30, 31, 32, 33]
  y = [ 1, 1,  1, 0, 0, 1, 0, 0, 1, 0 , 1 , 0 , 1 , 0 , 1]

  เพศ = {"ชาย":1, "หญิง":0}
  

  if len(x) == len(y):
    จำนวนข้อมูล = len(x)
    จำนวนชาย = y.count(เพศ['ชาย'])
    จำนวนหญิง = y.count(เพศ['หญิง'])
    
    เปอร์เซ็นต์ชาย = (จำนวนชาย / จำนวนข้อมูล) * 100
    เปอร์เซ็นต์หญิง = (จำนวนหญิง / จำนวนข้อมูล) * 100
    print("ข้อมูลทั้งหมด %d คน เป็นชาย %d คน และหญิง %d คน คิดเป็นร้อยละ %.2f%% และ %.2f%% ตามลำดับ"%(จำนวนข้อมูล, จำนวนชาย, จำนวนหญิง, เปอร์เซ็นต์ชาย, เปอร์เซ็นต์หญิง))

กิจกรรม_10()

ผลลัพธ์
ข้อมูลทั้งหมด 15 คน เป็นชาย 8 คน และหญิง 7 คน คิดเป็นร้อยละ 53.33% และ 46.67% ตามลำดับ

กิจกรรมที่ 11: เส้นโค้งปกติ \( f(z) = \frac{1}{\sqrt{2*\pi}} e^{\frac{-z^2}{2}} \)

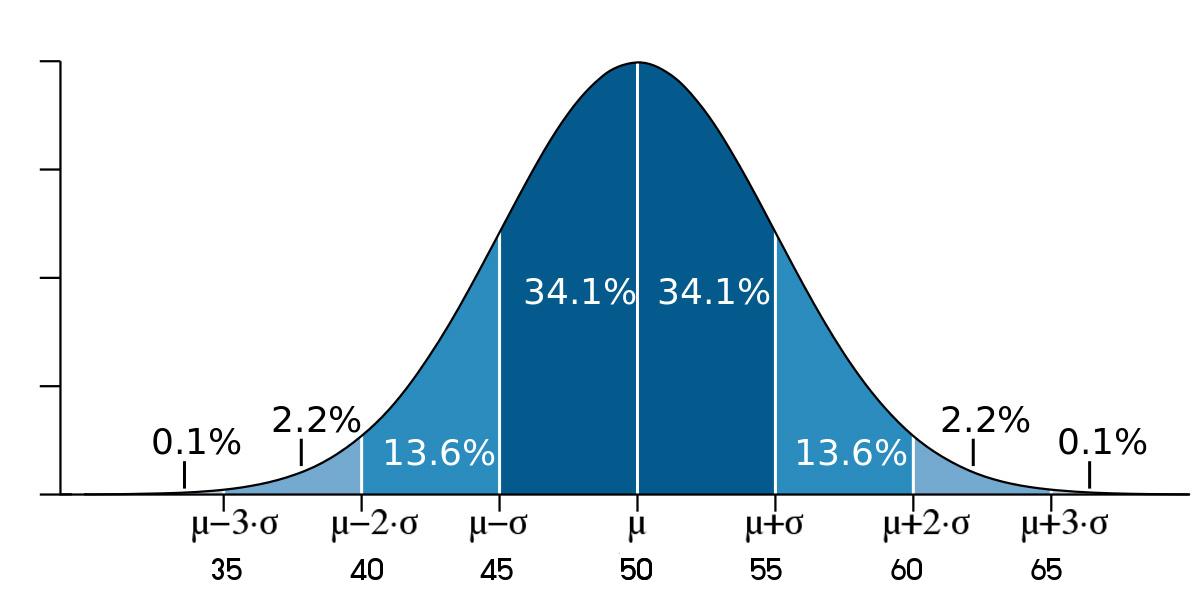
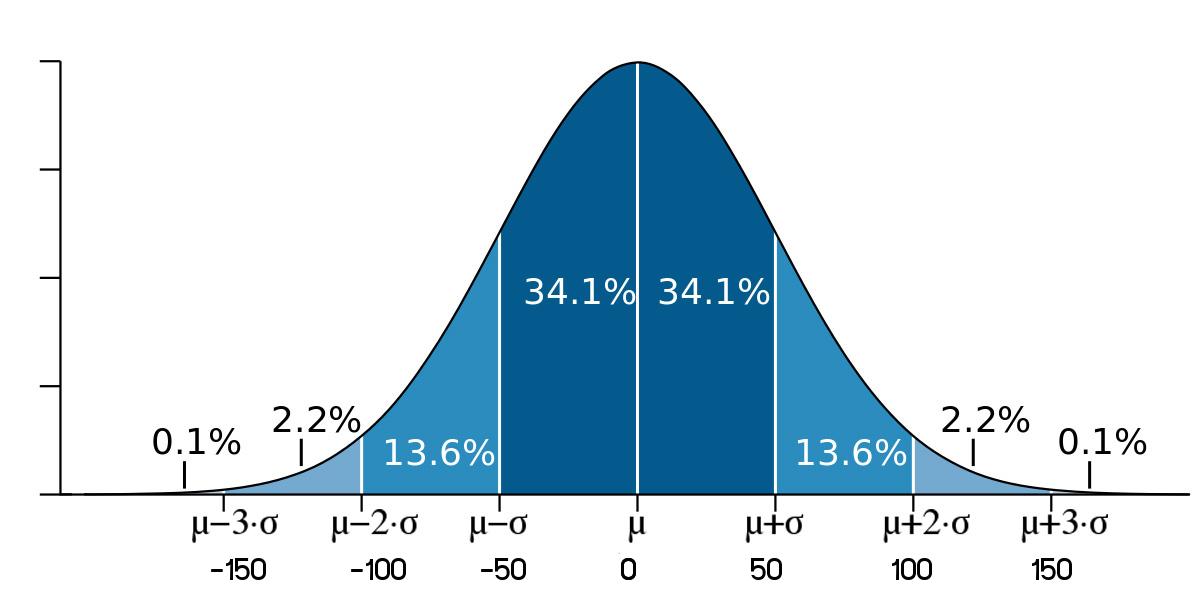
» การแจกแจงปกติมาตรฐาน เรียก Gaussian Function 
» เส้นโค้งปกติ หรือรูประฆังคว่ำ พบในข้อมูลธรรมชาติทั่วไป เช่น น้ำหนัก ส่วนสูง 
» เส้นโค้งปกติ ค่าเฉลี่ย มัธยฐาน และฐานนิยมจะมีค่าเท่ากัน
» \( \mu \) คือ ค่าเฉลี่ยของประชากร
» \( \sigma \) คือ ส่วนเบี่ยงเบนมาตรฐานของประชากร
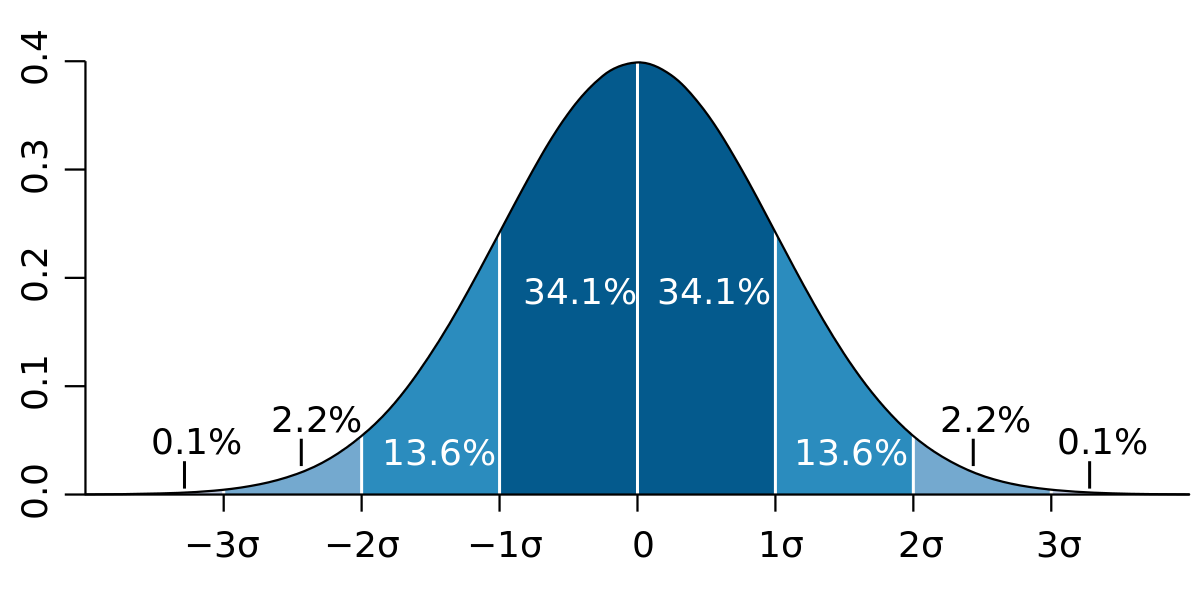
» เส้นโค้งปกติจะใช้ \( \sigma \) เป็นตัวแบ่งพื้นที่ได้ 8 ส่วน โดยมีค่า 1-3 ดังภาพ

» พื้นที่ใต้โค้งปกติระหว่าง 
- \( \mu - 1\sigma \) และ \( \mu + 1\sigma \) เท่ากับ 2x34.1 = 68.2%
- \( \mu - 2\sigma \) และ \( \mu + 2\sigma \) เท่ากับ 2x(34.1+13.6) = 95.4%
- \( \mu - 3\sigma \) และ \( \mu + 3\sigma \) เท่ากับ 2x(34.1+13.6+2.2) = 99.8%

การแปลงข้อมูลเป็นคะแนน Z (z-score) \( z = \frac{x-\mu}{\sigma} \)

เมื่อ \( x \) คือ ข้อมูลที่ต้องการแปลงเป็นคะแนน \( z \)
     \( \sigma \) คือ ค่าเบี่ยงเบนมาตรฐานของประชากร
     \( \mu \) คือ ค่าเฉลี่ยของประชากร

การหาค่าพื้นที่ใต้เส้นโค้งปกติด้วยการอินทิเกรต

from math import e,sqrt,pi
import scipy.integrate
f= lambda z: (1/sqrt(2*pi))*e**((-z**2)/2)
integrate = scipy.integrate.quad(f, -5, 5)
p = integrate[0]*100
print(p)

ผลลัพธ์
99.99994266968564

กิจกรรมที่ 12: จากกราฟแจงแจงปกติต่อไปนี้ จงตอบว่าค่า mean (\( \mu \)) และ sigma (\( \sigma \)) มีค่าเท่าไร

กิจกรรมที่ 13: สมมติว่าข้อมูลมีการแจกแจงปกติ มีค่าเฉลี่ย 300 และส่วนเบี่ยงเบนมาตรฐาน 100 จงคำนวณค่าต่อไปนี้

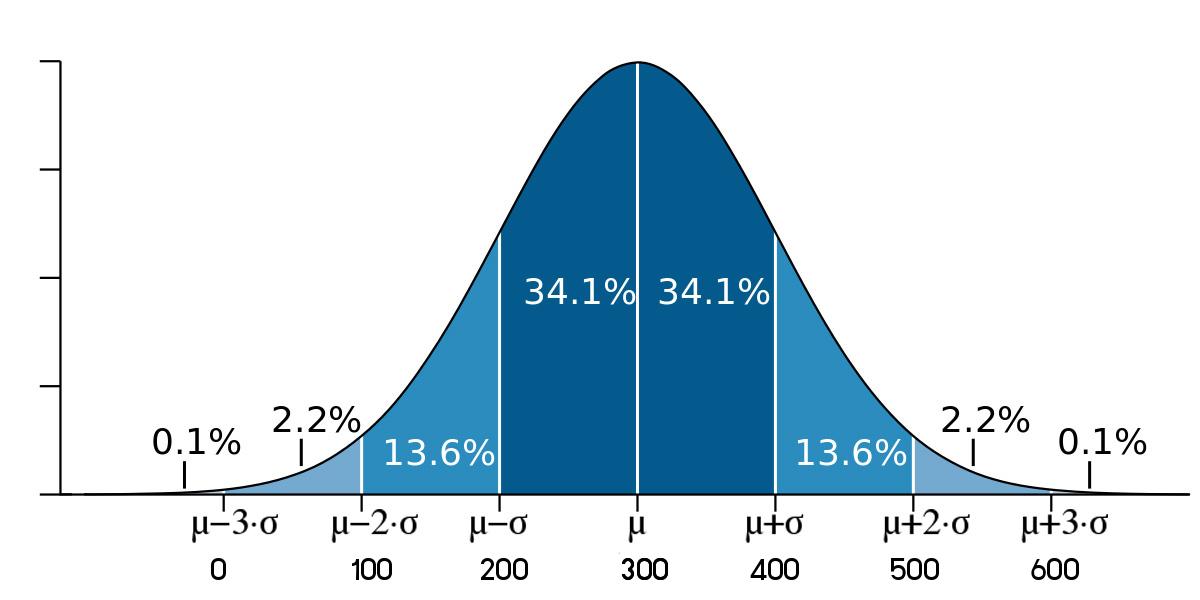
โจทย์กำหนด : ข้อมูลมีการแจกแจงปกติ มีค่าเฉลี่ย 300 คะแนนและส่วนเบี่ยงเบนมาตรฐาน 100 คะแนน จงหา
- ค่ามากกว่า 400 มีกี่เปอร์เซ็นต์  ตอบ : .............................................
- ค่าน้อยกว่า 500 มีกี่เปอร์เซ็นต์ ตอบ : ...............................................
- ค่าระหว่าง 200 และ 400 มีกี่เปอร์เซ็นต์ ตอบ : ...............................
- ค่าระหว่าง 100 และ 500 มีกี่เปอร์เซ็นต์ ตอบ : ...............................
- ค่าน้อยกว่า 100 มีกี่เปอร์เซ็นต์ ตอบ : ...............................................
- คนที่มีคะแนน 300 มีกี่เปอร์เซ็นต์ ตอบ :  ..........................................
- คนที่มีคะแนน 350 มีกี่เปอร์เซ็นต์ ตอบ : ...........................................

วิธีการคำนวณ คือ 
1. เขียนค่าเฉลี่ย ตรงกลางรูประฆังคว่ำ
2. ตำแหน่ง \(  \mu \pm 1 \times \sigma \) เท่ากับ 300-100 = 200 และ 300+100 = 400 ตามลำดับ นำตัวเลขดังกล่าวเขียนในช่อง \( \pm 1 \sigma \)
3. ตำแหน่ง  \(  \mu \pm 2 \times \sigma \) เท่ากับ 300-(2x100) = 100 และ 300+(2x100) = 500 ตามลำดับ นำตัวเลขดังกล่าวเขียนในช่อง \( \pm 2 \sigma \)
4. ตำแหน่ง  \(  \mu \pm 3 \times \sigma \) เท่ากับ 300-(3x100) = 0 และ 300+(3x100) = 600 ตามลำดับ นำตัวเลขดังกล่าวเขียนในช่อง \( \pm 2 \sigma \)
» ผลลัพธ์ที่ได้จะแสดงดังภาพต่อไปนี้

13.1.1 การคำนวณค่าเปอร์เซ็นต์ที่มากกว่าค่าที่กำหนดขึ้น

from math import e,sqrt,pi
import scipy.integrate
f= lambda z: (1/sqrt(2*pi))*e**((-z**2)/2)
mean = 300
sigma = 100
score = 400
z = (score - mean)/sigma
integrate = scipy.integrate.quad(f, -5, z)
p = 100 - integrate[0]*100
print("%.1f%%"%p)

ผลลัพธ์:
15.9%

13.1.2 การสร้างฟังก์ชั่นเพื่อคำนวณค่าเปอร์เซ็นต์ที่มากกว่าค่าที่กำหนดขึ้น

from math import e,sqrt,pi
import scipy.integrate

def การคำนวณค่าเปอร์เซ็นต์ที่มากกว่าค่าที่กำหนดขึ้น(mean,sigma,score):
    f= lambda z: (1/sqrt(2*pi))*e**((-z**2)/2)
    z = (score - mean)/sigma
    integrate = scipy.integrate.quad(f, -5, z)
    p = 100 - integrate[0]*100
    return p

test = การคำนวณค่าเปอร์เซ็นต์ที่มากกว่าค่าที่กำหนดขึ้น(300, 100, 400)
print("คนที่มีคะแนนมากกว่า 400 คิดเป็น %.1f เปอร์เซ็นต์"%test)

ผลลัพธ์:
คนที่มีคะแนนมากกว่า 400 คิดเป็น 15.9 เปอร์เซ็นต์

13.2.1 การคำนวณค่าเปอร์เซ็นต์ที่น้อยกว่าค่าที่กำหนดขึ้น

from math import e,sqrt,pi
import scipy.integrate
f= lambda z: (1/sqrt(2*pi))*e**((-z**2)/2)
mean = 300
sigma = 100
score = 200
z = (score - mean)/sigma
integrate = scipy.integrate.quad(f, -5, z)
p = integrate[0]*100
print("%.1f%%"%p)

ผลลัพธ์:
15.9%

13.2.2 การสร้างฟังก์ชั่นเพื่อคำนวณค่าเปอร์เซ็นต์ที่น้อยกว่าค่าที่กำหนดขึ้น

from math import e,sqrt,pi
import scipy.integrate

def การคำนวณค่าเปอร์เซ็นต์ที่มากกว่าค่าที่กำหนดขึ้น(mean,sigma,score):
    f= lambda z: (1/sqrt(2*pi))*e**((-z**2)/2)
    z = (score - mean)/sigma
    integrate = scipy.integrate.quad(f, -5, z)
    p = 100 - integrate[0]*100
    return p

test = การคำนวณค่าเปอร์เซ็นต์ที่น้อยกว่าค่าที่กำหนดขึ้น(300,100,200)
print("คนที่มีคะแนนน้อยกว่า %d คิดเป็น %.1f เปอร์เซ็นต์"%(200,test))

ผลลัพธ์:
คนที่มีคะแนนน้อยกว่า 200 คิดเป็น 15.9 เปอร์เซ็นต์

13.3.1 การเขียนโปรแกรมเพื่อคำนวณเปอร์เซ็นต์ของคะแนนที่อยู่ในช่วงที่กำหนด

» ค่าระหว่าง 200 และ 400 มีกี่เปอร์เซ็นต์
» ขั้นตอนการดำเนินการ 1) แปลงคะแนน 200 และ 400 เป็นคะแนน z 2) เปิดตาราง Z เพื่อหาค่าความน่าจะเป็นของทั้ง 2 ค่าออกมา 

from math import e,sqrt,pi
import scipy.integrate
f= lambda z: (1/sqrt(2*pi))*e**((-z**2)/2)
mean = 300
sigma = 100
score1 = 200
score2 = 400
z1 = (score1 - mean)/sigma
z2 = (score2 - mean)/sigma
integrate = scipy.integrate.quad(f, z1, z2)
p = integrate[0]*100
print("%.2f%%"%p)

ผลลัพธ์:
68.3%

13.3.2 การเขียนฟังก์ชั่นเพื่อคำนวณเปอร์เซ็นต์ของคะแนนที่อยู่ในช่วงที่กำหนด

from math import e,sqrt,pi
import scipy.integrate

def คำนวณเปอร์เซ็นต์ของคะแนนที่อยู่ในช่วงที่กำหนด(mean, sigma, score1, score2):
    f= lambda z: (1/sqrt(2*pi))*e**((-z**2)/2)
    z1 = (score1 - mean)/sigma
    z2 = (score2 - mean)/sigma
    integrate = scipy.integrate.quad(f, z1, z2)
    p = integrate[0]*100
    return p

test = คำนวณเปอร์เซ็นต์ของคะแนนที่อยู่ในช่วงที่กำหนด(300, 100, 200, 400)
print("เปอร์เซ็นต์ที่อยู่ในช่วงคะแนน %d ถึง %d มีค่า %.1f เปอร์เซ็นต์"%(200,400,test))

ผลลัพธ์:
เปอร์เซ็นต์ที่อยู่ในช่วงคะแนน 200 ถึง 400 มีค่า 68.3 เปอร์เซ็นต์

13.4.1 การคำนวณเปอร์เซ็นต์ของคะแนน

from math import e,sqrt,pi
import scipy.integrate
f= lambda z: (1/sqrt(2*pi))*e**((-z**2)/2)
mean = 300
sigma = 100
score = 400
z = (score - mean)/sigma
integrate = scipy.integrate.quad(f, -5, z)
p = integrate[0]*100
print("%.2f%%"%p)

ผลลัพธ์:
84.13%

13.4.2 การสร้างฟังก์ชั่นคำนวณเปอร์เซ็นต์ของคะแนน

from math import e,sqrt,pi
import scipy.integrate

def การคำนวณเปอร์เซ็นต์ของคะแนน(mean,sigma,score):
    f= lambda z: (1/sqrt(2*pi))*e**((-z**2)/2)
    z = (score - mean)/sigma
    integrate = scipy.integrate.quad(f, -5, z)
    p = integrate[0]*100
    return p

test = การคำนวณเปอร์เซ็นต์ของคะแนน(300,100,300)
print("คะแนน %d คิดเป็น %.1f เปอร์เซ็นต์"%(300,test))

ผลลัพธ์: คะแนน 300 คิดเป็น 50.0 เปอร์เซ็นต์

» ข้อมูลเพิ่มเติม : https://www.youtube.com/watch?v=nmiVpZR2Dd8

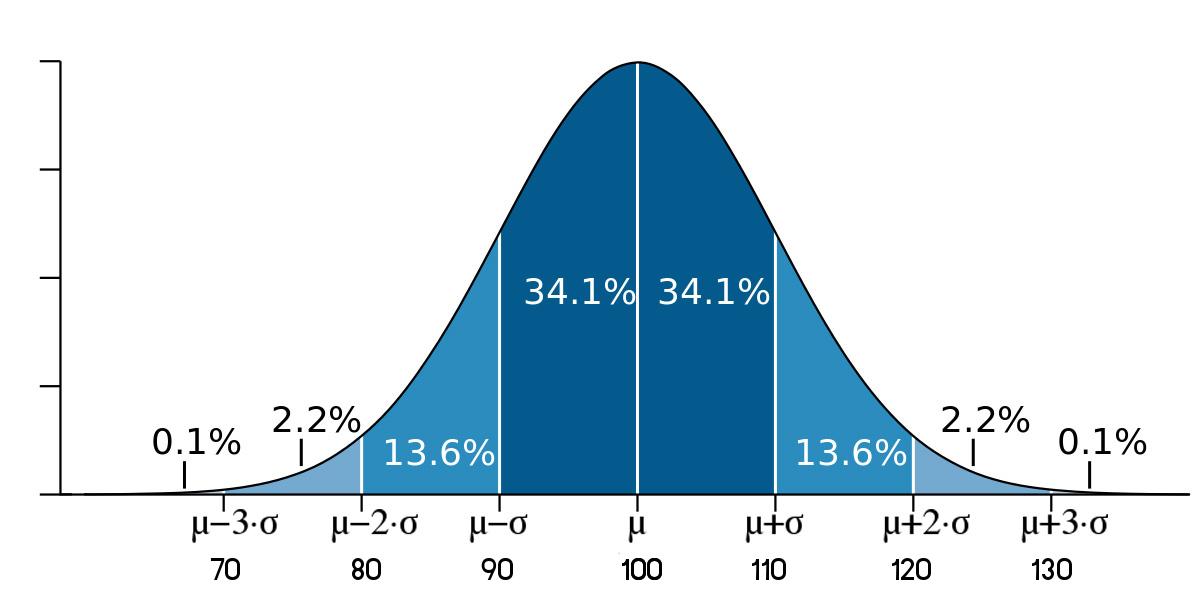
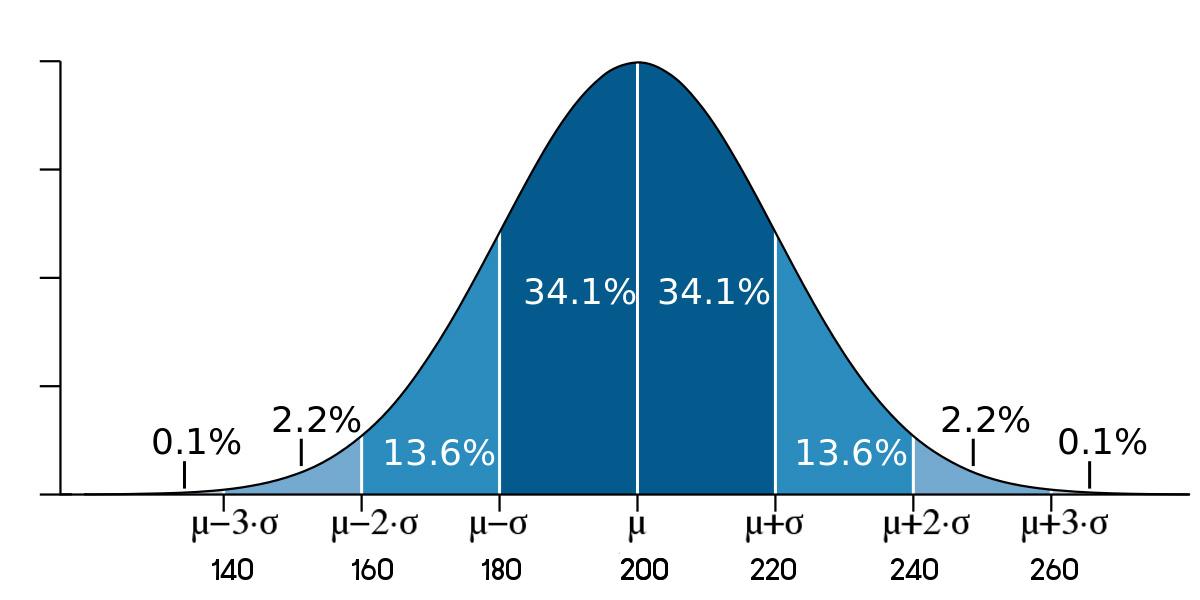
โจทย์ : การสอบ 1,000 คน คะแนนสอบแจกแจงปกติ ค่าเฉลี่ยคือ 200 และส่วนเบี่ยงเบนคือ 40 จงตอบคำถามต่อไปนี้

» ผู้ที่สอบได้คะแนนน้อยกว่า 200 คะแนน คิดเป็นกี่เปอร์เซ็นต์ ?
» ผู้สอบได้คะแนนระหว่าง 120 ถึง 240 คะแนน คิดเป็นกี่เปอร์เซ็นต์ ?
» ผู้สอบได้มากกว่า 320 คะแนนขึ้นไป คิดเป็นกี่เปอร์เซ็นต์ ?
» ผู้สอบได้มากกว่า 320 คะแนนขึ้นไป คิดเป็นกี่คน ? ................................ ( พื้นที่มากกว่า 320 ขึ้นไป x 1000 / 100)

กิจกรรมที่ 14 : การเปรียบเทียบตัวอย่างสองกลุ่มด้วย Chi Square

def transpose(l1):
    l2 = []
    for i in range(len(l1[0])):
        row =[]
        for item in l1:
            row.append(item[i])
        l2.append(row)
    return l2
 
    
ชาย = [26,13,5]
หญิง = [20,29,7]

data = [ชาย,หญิง]
alpha = 0.05

r = list(map(lambda a:sum(a), transpose(data)))
c = list(map(lambda a:sum(a), data))
total = sum(r)

E = []
for i in c:
    d = []
    for j in r:
        d.append(i*j/total)
    E.append(d)
    
df = (len(r) -1) * (len(c) -1)
print("Degree of Freedom : %d"%df)
    
chi2 = []
for i in range(len(data)):
    c=list(map(lambda a,b: ((b-a)**2)/b  ,data[i],E[i]))
    chi2.append(c)


CHI2 = sum(list(map(lambda x:sum(x), chi2)))
    
from scipy.stats import chi2
chi = chi2.isf(q=alpha, df=df)
if CHI2 < chi:
    print("ยอมรับ H0 ปฏิเสธ H1 ไม่แตกต่างกันชัวส์ 95%")
else:
    print("ยอมรับ H1 แตกต่างกันชัวส์ 95%")

กิจกรรมที่ 15 : การใช้ค่า T

การใช้ T-value 
1. ไม่รู้ค่า \( \sigma \)
2. ขนาดตัวอย่างข้อมูลน้อยกว่า 30 ชุด

สูตร \( \mu = \bar{x} \mp \frac{t \times s}{\sqrt{n}}\)

def ส่วนเบี่ยงเบนมาตรฐาน(data):
   n = len(data)
   mean = sum(data)/n
   sd = sqrt(sum(list(map(lambda i: ((i-mean)**2)/(n), data))))
   return sd


x = [83, 73, 62, 63, 71, 77, 77, 59, 92]
n = len(x)
mean = sum(x) / n
s = ส่วนเบี่ยงเบนมาตรฐาน(x)

» ค่า t เปิดจากตาราง df = n-1 และ ระดับความเชื่อมั่น 99% หรือ alpha = 0.01 (alpha level two tailed test) = 3.355

» แทนค่าตามสูตร \( \mu = \bar{x} \mp \frac{t \times s}{\sqrt{n}}\) เท่ากับ \( \mu = 73 \mp \frac{(3.355)(10.69)}{\sqrt{9}} \)
» \(\mu = 73 \mp 11.95 \) ดังนั้น \( \mu = (73-11.95, 73+11.95) = (61.05, 84.95) \) ที่ 99%

การเขียนโปรแกรมพยากรณ์และจัดหมวดหมู่ข้อมูล

การเรียนรู้ของเครื่องจักร (Machine Learning) แบ่งเป็น 2 แบบ คือ 
1 Supervise Learning คือการสอนแบบมีคำตอบ ใช้สำหรับการพยากรณ์ (Prediction)
2. Unsupervise Learning คือการสอนแบบไม่มีคำตอบ ใช้สำหรับหาความสัมพันธ์ของข้อมูล (Classification)

Linear Regression คือ พื้นฐานของอัลกอริทึมด้าน Machine Learning

- Linear Regession คือ การนำข้อมูลที่ได้มาคำนวณหาสมการเพื่อแทนลักษณะของข้อมูลนั้น ๆ

ลิเนียร์รีเกรสชั่นแบ่งเป็น 2 แบบ

- Simple Linear Regression คือ การนำข้อมูล 2 ชุด มาทำการหาสมการเพื่อแทนลักษณะข้อมูลของตัวแปรทั้ง 2 (ตัวแปรอิสระ 1 ตัวและตัวแปรตาม 1 ตัว)
- Multiple Linear Regression คือ การนำข้อมูลมากกว่า 2 ชุด มาทำการหาสมการเพื่อแทนลักษณะข้อมูลของตัวแปรทั้งหมด (ตัวแปรอิสระมากกว่า 1 ตัวและตัวแปรตาม 1 ตัว)

กิจกรรมที่ 16: การเขียนโปรแกรมคำนวณ Simple Linear Regression

» หลักการของ Simple Linear Regression คือ 
   1) ข้อมูลจะมีตัวแปรต้น 1 ตัว และตัวแปรตาม 1 ตัว
   2) เก็บรวบรวมข้อมูล ในตัวอย่างนี้วัดน้ำหนักหมี 10 ตัว และวัดขนาดเส้นรอบอกหมี ทั้ง 10 ตัว 
   3) ถ้าต้องการสร้างสูตรคำนวณเส้นรอบอกหมี ดังนั้น เส้นรอบอกหมีเรียกว่าตัวแปรตาม และน้ำหนักหมี เรียกว่าตัวแปรต้น
   4) ถ้าต้องการสร้างสูตรคำนวณน้ำหนักหมี ดังนั้น น้ำหนักหมีเรียกว่าตัวแปรตาม และเส้นรอบอกหมีเรียกว่าตัวแปรต้น
   5) คำนวณหา \( \beta_{0} \) และ \( \beta_{1} \)
   6) สูตรที่ได้อยู่ในรูป \( \hat{Y} = \beta_{0} + (\beta_{1} \times x) \)
   7) นำสูตรที่ได้ไปใช้พยากรณ์ เช่น ถ้าน้ำหนักหมี 100 Kg จะมีเส้นรอบอกหมีเท่าไร เป็นต้น
» สูตร Simple Linear Regression คือ  \( \hat{Y} =   \beta_{0} + (\beta_{1} \times x) \) 

\( \hat{Y} = \beta_{0} + \beta_{1} * x \)

\(\beta_{1} =\frac{ \sum{xy} - \frac{\sum{x}\sum{y}}{n}}{ \sum{x^2} - n (\bar{x})^2 }\)

\(\beta_{0} = \bar{y} - \beta_{1} (\bar{x}) \)

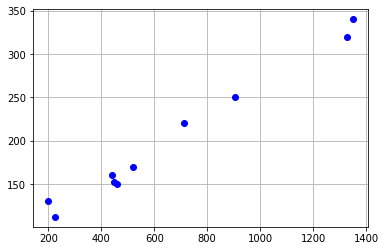
ตัวอย่าง : วัดน้ำหนักและรอบอกหมีจำนวน 10 ตัวได้ผลลัพธ์ดังนี้
ตัวที่  1 น้ำหนัก  225 กก ความยาวรอบอกเท่ากับ 112 ซม
ตัวที่  2 น้ำหนัก  200 กก ความยาวรอบอกเท่ากับ 130 ซม
ตัวที่  3 น้ำหนัก  458 กก ความยาวรอบอกเท่ากับ 150 ซม
ตัวที่  4 น้ำหนัก  448 กก ความยาวรอบอกเท่ากับ 152 ซม
ตัวที่  5 น้ำหนัก  440 กก ความยาวรอบอกเท่ากับ 160 ซม
ตัวที่  6 น้ำหนัก  520 กก ความยาวรอบอกเท่ากับ 170 ซม
ตัวที่  7 น้ำหนัก  712 กก ความยาวรอบอกเท่ากับ 220 ซม
ตัวที่  8 น้ำหนัก  905 กก ความยาวรอบอกเท่ากับ 250 ซม
ตัวที่  9 น้ำหนัก 1330 กก ความยาวรอบอกเท่ากับ 320 ซม
ตัวที่ 10 น้ำหนัก 1350 กก ความยาวรอบอกเท่ากับ 340 ซม

น้ำหนักและความยาวรอบอก คือ ตัวแปรที่ใช้สร้างสมการเส้นตรง (simple linear regression equation) 
- ถ้าให้น้ำหนักเป็นตัวแปรอิสระ ดังนั้น ความยาวรอบอกคือตัวแปรตาม
- ถ้าให้ความยาวรอบอกเป็นตัวแปรอิสระ ดังนั้น น้ำหนักจะเป็นตัวแปรตาม

นำค่าจากผลการทดลองมาสร้างตารางใหม่ ดังต่อไปนี้

n (ลำดับ)	x (น้ำหนักหมี)	y (เส้นรอบอกหมี)	x2	xy	y2
1	225	112	50,625	25,200	12,544
2	200	130	40,000	26,000	16,900
3	458	150	209,764	68,700	22,500
4	448	152	200,704	68,096	23,104
5	440	160	193,600	70,400	25,600
6	520	170	270,400	88,400	28,900
7	712	220	506,944	156,640	48,400
8	905	250	819,025	226,250	62,500
9	1330	320	1,768,900	425,600	102,400
10	1350	340	1,822,500	459,000	115,600
รวม	6,588	2,004	5,882,462	1,614,286	458,448

x = [225, 200, 458, 448, 440, 520, 712, 905, 1330, 1350]
y = [112, 130, 150, 152, 160, 170, 220, 250, 320, 340]

n = len(x)
xmean=sum(x)/len(x)
ymean=sum(y)/len(y)
x2 = list(map(lambda a:a**2, x))
y2 = list(map(lambda a:a**2, y))
xy = list(map(lambda a,b:a*b, x,y))

#print( sum(x), sum(y) , sum(x2), sum(xy), sum(y2))

B1 = (sum(xy) - ((sum(x)*sum(y)) / n)) / (sum(x2) - (n * (xmean**2)))
B0 = ymean - (B1*xmean)
print("สมการ Regression คือ : Y = %.2f + (%.2f * x)"%(B0,B1))

ผลลัพธ์ : 
สมการ Regression คือ : Y = 74.79 + (0.19 * x)

การนำสมการ (model) มาใช้พยากรณ์ เช่น ถ้าหมีตัวหนึ่งมีน้ำหนัก 250 กก จะทำนายว่าหมีตัวนี้มีความยาวรอบอกเท่าใด คำนวณได้ดังนี้

B0 = 74.793941
B1 = 0.190659
ความยาวรอบอก = B0 + (B1 * 250)
print("หมีหนัก 250 กก ทายว่ามีเส้นรอบอก %d ซม"%ความยาวรอบอก)

ผลลัพธ์ :
หมีหนัก 250 กก ทายว่ามีเส้นรอบอก 122 ซม

กิจกรรมที่ 17: (ตัวอย่าง 2) การศึกษาเรื่องแรงดึงของกาวในการยึดชิ้นงานเข้าด้วยกันด้วย Simple Linear Regression

» การศึกษาเรื่องแรงดึงของกาวในการยึดชิ้นงานเข้าด้วยกัน 
» ขั้นตอน คือ ทากาวลงบนชิ้นงานทั้งสองชิ้นจากนั้นนำมาติดเข้าด้วยกัน  จากนั้นนำไปอบเพื่อให้กาวแห้งติดกัน 
» ผู้ศึกษาต้องการทราบความสัมพันธ์ระหว่าง อุณหภูมิที่ใช้อบ กับแรงดึงของกาว โดยทดลอง 3 ตัวอย่าง
» รอบที่ 1 ใช้ตัวอย่าง 3 ชิ้น โดยให้ความร้อน 70°C เวลาอบ 15 นาที นำไปวางในอุณหภูมิห้อง 20 นาที นำไปทดสอบแรงดึงจนชิ้นงานฉีกขาดออกจากกัน ทนแรงได้ 2.3 2.6 และ 2.1 ตามลำดับ
» รอบที่ 2 ใช้ตัวอย่าง 3 ชิ้น โดยให้ความร้อน 80°C เวลาอบ 15 นาที นำไปวางในอุณหภูมิห้อง 20 นาที นำไปทดสอบแรงดึงจนชิ้นงานฉีกขาดออกจากกัน ทนแรงได้ 2.5 2.9 และ 2.4 ตามลำดับ
» รอบที่ 3 ใช้ตัวอย่าง 3 ชิ้น โดยให้ความร้อน 90°C เวลาอบ 15 นาที นำไปวางในอุณหภูมิห้อง 20 นาที นำไปทดสอบแรงดึงจนชิ้นงานฉีกขาดออกจากกัน ทนแรงได้ 3.0 3.1 และ 2.8 ตามลำดับ
» รอบที่ 4 ใช้ตัวอย่าง 3 ชิ้น โดยให้ความร้อน 100°C เวลาอบ 15 นาที นำไปวางในอุณหภูมิห้อง 20 นาที นำไปทดสอบแรงดึงจนชิ้นงานฉีกขาดออกจากกัน ทนแรงได้ 3.3 3.5 และ 3.0 ตามลำดับ

ผลการทดลอง

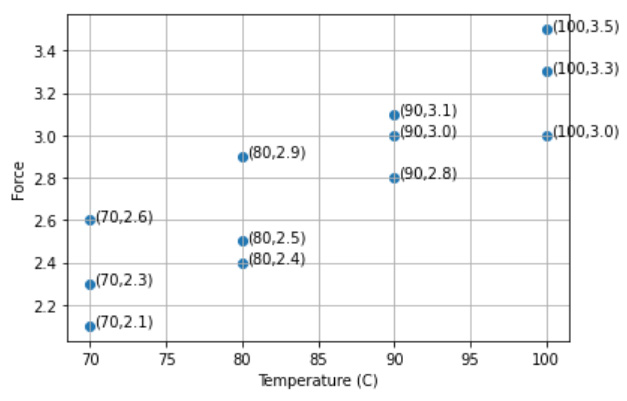
พล็อตกราฟข้อมูล

import numpy as np
import matplotlib.pyplot as plt
np.random.seed(19680801)
x = [70,70,70,80,80,80,90,90,90,100,100,100]
y = [2.3,2.6,2.1,2.5,2.9,2.4,3.0,3.1,2.8,3.3,3.5,3.0]
plt.grid(1)
plt.xlabel("Temperature (C)")
plt.ylabel("Force")
plt.scatter(x, y)
plt.show()

การพล็อตพิกัดลงบนกราฟ

for i in range(len(x)):
  txt = "(%d,%.1f)"%(x[i],y[i])
  plt.annotate(txt, (x[i]+0.3, y[i]))

นำค่าจากผลการทดลองมาสร้างตารางใหม่ ดังต่อไปนี้

n	x	y	x2	xy	y2
1	70	2.3	4900	161	5.29
2	70	2.6	4900	182	6.76
3	70	2.1	4900	147	4.41
4	80	2.5	6400	200	6.25
5	80	2.9	6400	232	8.41
6	80	2.4	6400	192	5.76
7	90	3.0	8100	270	9.00
8	90	3.1	8100	279	9.61
9	90	2.8	8100	252	7.84
10	100	3.3	10000	330	10.89
11	100	3.5	10000	350	12.25
12	100	3.0	10000	300	9.00
Sum	1020	33.5	88200	2895	95.47

การเขียนโปรแกรมคำนวณผลรวมของตัวแปร \( x \) \( y \) \( x^2 \) \( xy \) และ \( y^2 \)

x = [70,70,70,80,80,80,90,90,90,100,100,100]
y = [2.3,2.6,2.1,2.5,2.9,2.4,3.0,3.1,2.8,3.3,3.5,3.0]
xmean=sum(x)/len(x)
ymean=sum(y)/len(y)
x2 = list(map(lambda a:a**2, x))
y2 = list(map(lambda a:a**2, y))
xy = list(map(lambda a,b:a*b, x,y))

print( sum(x), sum(y) , sum(x2), sum(xy), sum(y2))

ผลลัพธ์
1020 33.5 88200 2895.0 95.47

การเขียนโปรแกรมคำนวณค่า \( \beta_{0} \) และ \( \beta_{1} \) และแทนค่าในสมการ Simple Linear Regression \( \hat{Y} = \beta_{0} + (\beta_{1} \times x) \)

» ให้ทำการเขียนโปรแกรมคำนวณ \( \beta_{1} \) จากนั้นนำไปแทนค่าใน \( \beta_{0} \)
» นำค่า \( \beta_{1} \) และ \( \beta_{0} \) แทนค่าในสมการ Simple Linear Regression \( \hat{Y} =   \beta_{0} + (\beta_{1} \times x) \) 

แทนค่าเพื่อคำนวณหาค่า \( \beta_{1} \) จากสูตร \( \beta_{1} = \frac{ \sum{xy} - \frac{\sum{x} \sum{y} }{n} }{ \sum{x^2} - n(\bar{x})^2 } \)

B1 = (sum(xy) - ((sum(x)*sum(y)) / n)) / (sum(x2) - (n * (xmean**2)))
print(B1)

ผลลัพธ์
0.03166666666666667

แทนค่าเพื่อคำนวณหาค่า \( \beta_{0} \) จากสูตร \( \beta_{0} = \bar{y} - \beta_{1} (\bar{x}) \)

B0 = ymean - (B1*xmean)
print(B0)

ผลลัพธ์
0.099999999

การเขียนโปรแกรมแทนค่าในสมการ Simple Linear Regression \( \hat{Y} = \beta_{0} + (\beta_{1} \times x) \)

predict = B0 + (B1 * new_x)

การพยากรณ์ค่าแรงดึงที่อุณหภูมิต่าง ๆ ด้วยสูตร Simple Linear Regression ที่สร้างขึ้นจากข้อมูลที่ได้จากการทดลอง \( \hat{Y} = 0.1 + (0.0316 \times x) \)

for i in range(70,101):
  predict = B0 + (B1 * i)
  print("อบชิ้นงานที่อุณหภูมิ %d°C จะทนแรงดึงได้ %.2f"%(i, predict))

ผลลัพธ์
อบชิ้นงานที่อุณหภูมิ 70°C จะทนแรงดึงได้ 2.32
อบชิ้นงานที่อุณหภูมิ 71°C จะทนแรงดึงได้ 2.35
อบชิ้นงานที่อุณหภูมิ 72°C จะทนแรงดึงได้ 2.38
อบชิ้นงานที่อุณหภูมิ 73°C จะทนแรงดึงได้ 2.41
อบชิ้นงานที่อุณหภูมิ 74°C จะทนแรงดึงได้ 2.44
อบชิ้นงานที่อุณหภูมิ 75°C จะทนแรงดึงได้ 2.47
อบชิ้นงานที่อุณหภูมิ 76°C จะทนแรงดึงได้ 2.51
อบชิ้นงานที่อุณหภูมิ 77°C จะทนแรงดึงได้ 2.54
อบชิ้นงานที่อุณหภูมิ 78°C จะทนแรงดึงได้ 2.57
อบชิ้นงานที่อุณหภูมิ 79°C จะทนแรงดึงได้ 2.60
อบชิ้นงานที่อุณหภูมิ 80°C จะทนแรงดึงได้ 2.63
อบชิ้นงานที่อุณหภูมิ 81°C จะทนแรงดึงได้ 2.67
อบชิ้นงานที่อุณหภูมิ 82°C จะทนแรงดึงได้ 2.70
อบชิ้นงานที่อุณหภูมิ 83°C จะทนแรงดึงได้ 2.73
อบชิ้นงานที่อุณหภูมิ 84°C จะทนแรงดึงได้ 2.76
อบชิ้นงานที่อุณหภูมิ 85°C จะทนแรงดึงได้ 2.79
อบชิ้นงานที่อุณหภูมิ 86°C จะทนแรงดึงได้ 2.82
อบชิ้นงานที่อุณหภูมิ 87°C จะทนแรงดึงได้ 2.85
อบชิ้นงานที่อุณหภูมิ 88°C จะทนแรงดึงได้ 2.89
อบชิ้นงานที่อุณหภูมิ 89°C จะทนแรงดึงได้ 2.92
อบชิ้นงานที่อุณหภูมิ 90°C จะทนแรงดึงได้ 2.95
อบชิ้นงานที่อุณหภูมิ 91°C จะทนแรงดึงได้ 2.98
อบชิ้นงานที่อุณหภูมิ 92°C จะทนแรงดึงได้ 3.01
อบชิ้นงานที่อุณหภูมิ 93°C จะทนแรงดึงได้ 3.04
อบชิ้นงานที่อุณหภูมิ 94°C จะทนแรงดึงได้ 3.08
อบชิ้นงานที่อุณหภูมิ 95°C จะทนแรงดึงได้ 3.11
อบชิ้นงานที่อุณหภูมิ 96°C จะทนแรงดึงได้ 3.14
อบชิ้นงานที่อุณหภูมิ 97°C จะทนแรงดึงได้ 3.17
อบชิ้นงานที่อุณหภูมิ 98°C จะทนแรงดึงได้ 3.20
อบชิ้นงานที่อุณหภูมิ 99°C จะทนแรงดึงได้ 3.23
อบชิ้นงานที่อุณหภูมิ 100°C จะทนแรงดึงได้ 3.27

อัลกอริทึมการเรียนรู้ของเครื่องจักร (Machine Learning)

อัลกอริทึมการเรียนรู้ของเครื่อง ได้แก่
- Simple Linear Regression
- Multiple Linear Regression
- Decision Tree (C.45)
- Support Vector Machine (SVM) 
- Artificial Neural Network (ANN) 
- ฯลฯ

คำศัพท์ที่เกี่ยวข้องกับ Machine Learning

1. คุณลักษณะเด่น (Feature) จากตัวอย่างที่ผ่านมาลักษณะเด่น คือ น้ำหนักหมี
2. คลาส (Class) เรียกอีกอย่างว่า Target หรือ Label คือ คำตอบ ในตัวอย่างที่ผ่านมาคือ  เส้นรอบอก

กิจกรรมที่ 18: การจัดหมวดหมู่ผลไม้ชนิดต่าง ๆ ด้วย Decision Tree

น้ำหนักหน่วยเป็นกรัม (weight)	สี (Color)	ชนิดผลไม้ (Label)
320.5	เปลือกสีเขียว	มะละกอ
315	เปลือกสีเขียว	มะละกอ
210	เปลือกสีเขียว	มะละกอ
350.2	เปลือกสีเขียว	มะละกอ
300.1	เปลือกสีเขียว	มะละกอ
12.2	เปลือกสีส้ม	ผลส้ม
14.3	เปลือกสีส้ม	ผลส้ม
10.6	เปลือกสีส้ม	ผลส้ม
11.3	เปลือกสีส้ม	ผลส้ม
20.1	เปลือกสีเหลือง	กล้วย
21.3	เปลือกสีเหลือง	กล้วย
22.4	เปลือกสีเหลือง	กล้วย
23	เปลือกสีเหลือง	กล้วย

คำถาม : 
- คุณลักษณะเด่น (Feature) คือ ....................................................................................... (ตอบ : น้ำหนัก และ สี)
- คลาส (Class) หรือ Label หรือ Target คือ ................................................................. (ตอบ : ชนิดผลไม้)

เขียนโปรแกรมเพื่อสร้างโมเดลการพยากรณ์ด้วย Decition Tree ได้ดังนี้

from sklearn import tree

#แทน 1 คือ สีเขียว, 2 คือ สีส้ม และ 3 คือสีเหลือง
features = [[320.5, 1], [315, 1], [210, 1], [350.2, 1], [300.1, 1], [12.2, 2], [14.3, 2], [10.5, 2], [11.2, 2], [11.1, 2], [20, 3], [21.2, 3], [22.2, 3], [23, 3]] 

labels = ["มะละกอ", "มะละกอ", "มะละกอ", "มะละกอ", "มะละกอ", "ส้ม", "ส้ม", "ส้ม", "ส้ม", "ส้ม", "กล้วย", "กล้วย", "กล้วย", "กล้วย"]

classifier = tree.DecisionTreeClassifier()

classifier.fit(features, labels)

# เมื่อต้องการทราบว่า ของสิ่งหนึ่งที่มีน้ำหนัก 310 และมีสีเขียว คือ อะไร เขียนโปรแกรมเพื่อให้ตัว classifier (ตัวจัดหมวดหมู่) จะเขียนได้ดังนี้
print(classifier.predict([[310, 1]])[0])

ผลลัพธ์ :
มะละกอ

 หมายเหตุ : ให้ติดตั้งไลบรารี่ Scikit-Learn ด้วยคำสั่ง !pip install sklearn
- โปรแกรม Scikit-Learn เป็นไลบรารี่ด้านการเรียนรู้ของเครื่องจักร (machine learning) สำหรับภาษาไพธอน

กิจกรรมที่ 19: การเขียนโปรแกรมจัดหมวดหมู่ภาพทะเลหรือภาพภูเขา

mahotas เป็นไลบรารี่การประมวลผลภาพ (Image Processing) ใช้สกัดคุณลักษณะเด่นภายในภาพ ติดตั้งด้วยคำสั่ง !pip install mahotas

ภาพที่ใช้สำหรับสอน (Train)

ภาพที่ใช้สำหรับทดสอบ (Test)

%pylab inline
import mahotas as mh

features = []
labels = []

im1 = mh.imread("img/sea1.jpg")
im1 = mh.colors.rgb2gray(im1, dtype=np.uint8)
features.append(mh.features.haralick(im1).ravel())

im2 = mh.imread("img/sea2.jpg")
im2 = mh.colors.rgb2gray(im2, dtype=np.uint8)
features.append(mh.features.haralick(im2).ravel())

im3 = mh.imread("img/sea3.jpg")
im3 = mh.colors.rgb2gray(im3, dtype=np.uint8)
features.append(mh.features.haralick(im3).ravel())

im4 = mh.imread("img/sea4.jpg")
im4 = mh.colors.rgb2gray(im4, dtype=np.uint8)
features.append(mh.features.haralick(im4).ravel())

im5 = mh.imread("img/sea5.jpg")
im5 = mh.colors.rgb2gray(im5, dtype=np.uint8)
features.append(mh.features.haralick(im5).ravel())


im6 = mh.imread("img/mountain1.jpg")
im6 = mh.colors.rgb2gray(im6, dtype=np.uint8)
features.append(mh.features.haralick(im6).ravel())

im7 = mh.imread("img/mountain2.jpg")
im7 = mh.colors.rgb2gray(im7, dtype=np.uint8)
features.append(mh.features.haralick(im7).ravel())

im8 = mh.imread("img/mountain3.jpg")
im8 = mh.colors.rgb2gray(im8, dtype=np.uint8)
features.append(mh.features.haralick(im8).ravel())

im9 = mh.imread("img/mountain4.jpg")
im9 = mh.colors.rgb2gray(im9, dtype=np.uint8)
features.append(mh.features.haralick(im9).ravel())


labels = ['sea','sea','sea','sea','sea','mountain','mountain','mountain','mountain']
features = np.array(features)
labels = np.array(labels)


from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
clf = Pipeline([('preproc', StandardScaler()),('classifier', LogisticRegression())])

clf.fit(features,labels)

#from sklearn import cross_validation
#cv = cross_validation.LeaveOneOut(len(labels))
#scores = cross_validation.cross_val_score(clf, features, labels, cv=cv)
#print('Accuracy: {:.1%}'.format(scores.mean()))

test = mh.imread("img/test1.jpg")
test = mh.colors.rgb2gray(test, dtype=np.uint8)
test_feature = mh.features.haralick(test).ravel()

print(clf.predict([test_feature]))

test = mh.imread("img/test2.jpg")
test = mh.colors.rgb2gray(test, dtype=np.uint8)
test_feature = mh.features.haralick(test).ravel()

print(clf.predict([test_feature]))

ผลลัพธ์ : 
['sea']
['mountain']

รายชื่อการเข้าเรียนและส่งงาน

» ไม่พบกิจกรรมการเรียนในสัปดาห์นี้ กรุณาตรวจสอบเวลา : วันนี้ คือ วันที่ 16-07-2025

รายชื่อการเข้าเรียนและส่งงาน

» ไม่พบกิจกรรมการเรียนในสัปดาห์นี้ กรุณาตรวจสอบเวลา : วันนี้ คือ วันที่ 16-07-2025